��Ŀ����
�������������( )
A. ��ǵIJ���һ���Ƕ۽� B. һ����Ǻ�һ���۽�һ������
C. ���������Dz��ܶ��Ƕ۽� D. ��������ȵ����Ƕ���45��
 B
��������A. �����С��90�㣬�� ��ǵIJ���һ���Ƕ۽ǣ�����ȷ��
B. ���磺30��+100��=130�㣬��һ����Ǻ�һ���۽Dz�һ���������ʲ���ȷ��
C. ����������Ƕ��Ƕ۽ǣ�����;ʹ���180�㣬��������Dz��ܶ��Ƕ۽ǣ�����ȷ��
D. ��������ȵ����Ƕ���45�㣬����ȷ��
��ѡB.
B
��������A. �����С��90�㣬�� ��ǵIJ���һ���Ƕ۽ǣ�����ȷ��
B. ���磺30��+100��=130�㣬��һ����Ǻ�һ���۽Dz�һ���������ʲ���ȷ��
C. ����������Ƕ��Ƕ۽ǣ�����;ʹ���180�㣬��������Dz��ܶ��Ƕ۽ǣ�����ȷ��
D. ��������ȵ����Ƕ���45�㣬����ȷ��
��ѡB.
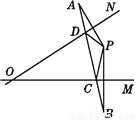
��ͼ,��֪��PΪ��MON��һ��,��P���A����ֱ��ON�Գ�,��P���B����ֱ��OM�Գ�.����AB,��ON��D��,��OM��C��,��AB��Ϊ15 cm,���PCD���ܳ�.
 15 cm.
���������ɵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƿɵã�ON��ֱƽ��AP��OM��ֱƽ��BP�����ݴ�ֱƽ���ߵ����ʿɵ�DA=DP��CP=CB��ͨ�����������õ���PCD���ܳ���AB��������ϵ���������.
��������
�ߵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƣ�
��ON��ֱƽ��AP��OM��ֱƽ��BP��
��DA=DP��CP=CB��
��...
15 cm.
���������ɵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƿɵã�ON��ֱƽ��AP��OM��ֱƽ��BP�����ݴ�ֱƽ���ߵ����ʿɵ�DA=DP��CP=CB��ͨ�����������õ���PCD���ܳ���AB��������ϵ���������.
��������
�ߵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƣ�
��ON��ֱƽ��AP��OM��ֱƽ��BP��
��DA=DP��CP=CB��
��... ��ͼ������ABCD�У�AB��2AD��EΪAD���е㣬EF��EC��AB�ڵ�F������FC.
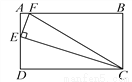
(1)��֤����AEF�ס�DCE��
(2)��tan��ECF��ֵ��
 ��1���𰸼���������2��
����������1�����ݾ��ε����ʿ�֪��A="��D" =90�㣬�ٸ��������ε��ڽǺ�Ϊ180�㣬��֪��DCE+��DEC=900������֪EF��EC���ɵã���AEF+��DEC=900�ó���DCE=��AEF������֤���SAEF�רSDCE
��2���ɣ�1����֪���SAEF�רSDCE ��=
�ھ���ABCD�У�EΪAD ���е㡣
AB=2AD �� DC=AB=4AE �� ...
��1���𰸼���������2��
����������1�����ݾ��ε����ʿ�֪��A="��D" =90�㣬�ٸ��������ε��ڽǺ�Ϊ180�㣬��֪��DCE+��DEC=900������֪EF��EC���ɵã���AEF+��DEC=900�ó���DCE=��AEF������֤���SAEF�רSDCE
��2���ɣ�1����֪���SAEF�רSDCE ��=
�ھ���ABCD�У�EΪAD ���е㡣
AB=2AD �� DC=AB=4AE �� ... ��������֤��������գ�
��ͼ����֪BD��AC��EF��AC��D��F�ֱ�Ϊ���㣬�ҡ�1=��4����֤����ADG=��C
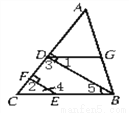
֤������BD��AC��EF��AC
���2=��3=90�㣨 ��
��BD��EF ( )
���4=_____( )
�ߡ�1=��4
���1=_____( )
��DG��BC( )
���ADG=��C( )
 ������
������������������������Ҫ��Ϥƽ���ߵ����ʺ��ж�������ȷ���������������ɣ���Ҫע��ƽ���ߵ����ʺ��ж����ۺ����ã�
�����������BD��AC��EF��AC����֪����
���2=��3=90�㣬
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���4=��5����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�1=��4����֪����
���1=��5��������������
��DG��BC���ڴ�����...
������
������������������������Ҫ��Ϥƽ���ߵ����ʺ��ж�������ȷ���������������ɣ���Ҫע��ƽ���ߵ����ʺ��ж����ۺ����ã�
�����������BD��AC��EF��AC����֪����
���2=��3=90�㣬
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���4=��5����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�1=��4����֪����
���1=��5��������������
��DG��BC���ڴ�����... ��ͼ��ֱ��AB��CD�ཻ�ڵ�O��EF��AB��O���ҡ�COE=50�㣬���BOD���ڣ�������
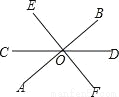
A. 40�� B. 45�� C. 55�� D. 65��
 A
����������EF��AB��O����COE=50�㣬
���AOC=90��-50��=40�㣬
�ߡ�AOC���BOD�ǶԶ��ǣ�
���BOD=��AOC=40�㣻
��ѡA��
A
����������EF��AB��O����COE=50�㣬
���AOC=90��-50��=40�㣬
�ߡ�AOC���BOD�ǶԶ��ǣ�
���BOD=��AOC=40�㣻
��ѡA�� ��ͼ����֪AB��CD����1=100�㣬��2=120�㣬��Ϧ�=_____.
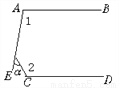
 40��
��������
�ӳ�AE��DC�ཻ�ڵ�F.
��AB��CD����1=100�㣬
���F=180��-100��=80�㣬
��Ϧ�=��2-��F=120��-80��=40��.
40��
��������
�ӳ�AE��DC�ཻ�ڵ�F.
��AB��CD����1=100�㣬
���F=180��-100��=80�㣬
��Ϧ�=��2-��F=120��-80��=40��. ��֪��AOB=40�㣬OCƽ�֡�AOB�����AOC�IJ��ǵ���_____.
 160��
��������
��OCƽ�֡�AOB����AOB=40�㣬
��,
���AOC�IJ���=180��-20��=160��.
160��
��������
��OCƽ�֡�AOB����AOB=40�㣬
��,
���AOC�IJ���=180��-20��=160��. ��֪(x2��px��8)(x2��3x��q)��չ��ʽ�в���x2��x3���p��q��ֵ��
 p��3��q��1.
�����������������������ʽ�ij˷���������ɺ��ݲ������ϵ��Ϊ0��⼴��.
����������ߣ�x2+px+8����x2��3x+q��
=x4��3x3+qx2+px3��3px2+pqx+8x2��24x+8q
=x4+��p��3��x3+��q��3p+8��x2+��pq��24��x+8q��
�߳˻��в���x2��x3�
��p��3=0��q��3p+8=0��
��p=...
p��3��q��1.
�����������������������ʽ�ij˷���������ɺ��ݲ������ϵ��Ϊ0��⼴��.
����������ߣ�x2+px+8����x2��3x+q��
=x4��3x3+qx2+px3��3px2+pqx+8x2��24x+8q
=x4+��p��3��x3+��q��3p+8��x2+��pq��24��x+8q��
�߳˻��в���x2��x3�
��p��3=0��q��3p+8=0��
��p=... ����ͼ���У���Գ�ͼ���У� ��




A. 1�� B. 2�� C. 3�� D. 4��
 A
����������������
�������ĸ�ͼ���У�ֻ�е�һ������Գ�ͼ�Σ�������Ȼ�����ǣ��������ڲ�ͼ�β��ǣ���ѡA��
A
����������������
�������ĸ�ͼ���У�ֻ�е�һ������Գ�ͼ�Σ�������Ȼ�����ǣ��������ڲ�ͼ�β��ǣ���ѡA�� 
