题目内容
下列命题正确的是（ ）
A．内错角相等
B．相等的角是对顶角
C．三条直线相交 ，必产生同位角、内错角、同旁内角
D．同位角相等，两直线平行
D．
【解析】
试题分析：A．只有两直线平行，内错角才相等，故错误；
B．对顶角相等，但相等的角不一定是对顶角，故错误；
C．必须出现“三线八角”的形式，即两直线被第三条直线所截，才产生同位角，内错角，同旁内角，故错误；
D．平行线的判定定理，故正确．
故选D．
如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．
求证：（1）FC＝AD；
（2）AB＝BC＋AD．
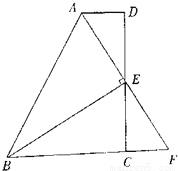
（1）证明见解析；（2）证明见解析.
【解析】试题分析:（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答．
（2）根据线段垂直平分线的性质判断出AB=BF即可．
证明：（1）∵AD∥BC（已知），
∴∠ADC=∠ECF（两直线平行，内错角相等），
∵E是CD的中点（已知），
∴DE=EC（中点... 阅读下面的材料，再回答问题：
三角函数中常用公式sin(A＋B)＝sinAcosB＋cosAsinB，求sin(A＋B)的值．
例如：sin75°＝sin(45°＋30°)＝sin45°cos30°＋cos45°sin30°＝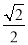
×
＋
×
＝
＋
＝
.
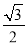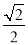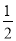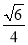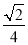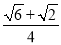试用公式cos(A＋B)＝cosAcosB－sinAsinB，求cos75°的值．
【解析】试题分析：将cos75°变为cos(45°+30°)，然后按所给的公式进行计算即可.
试题解析：cos75°＝cos(45°＋30°)＝cos45°cos30°－sin45°sin30°=. 阅读下面的证明过程，指出其错误.
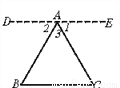
已知△ABC
求证：∠A+∠B+∠C=180°
证明：过A作DE∥BC，且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行，内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°
答案见解析
【解析】试题分析：注意作辅助线的方法，过点A作的辅助线不能同时满足两个条件．只能作平行线后，根据平行线的性质得到∠1=∠C．
错误①：过A作DE∥BC，且使∠1=∠C，应改为：过A作DE∥BC.
错误②：∵∠1=∠C(画图)，理由错，应改为：两直线平行，内错角相等. 如图，若AB∥CD，则∠A、∠E、∠D之间的关系是( )
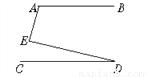
A. ∠A+∠E+∠D=180° B. ∠A－∠E+∠D=180°
C. ∠A+∠E－∠D=180° D. ∠A+∠E+∠D=270°
C
【解析】过点E作EF∥CD，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=180°-∠A,∠DEF=∠D，
∴∠AED=∠AEF+∠DEF=180°-∠A+∠D；
即∠AED+∠A-∠D =180°.
故选C. 如图,DAE是一条直线,DE∥BC，则∠BAC=___度.
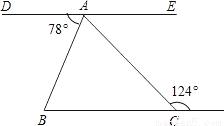
46°．
【解析】试题分析：∵DE∥BC，∴∠DAC=124°，∴∠BAC=∠DAC﹣∠DAB=124°﹣78°=46°．故答案为：46°． 如图，若l1∥l2，∠1=45°，则∠2=_____.
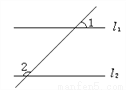
135
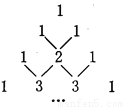
【解析】试题分析：根据对顶角的性质求出∠1的对顶角，然后根据两直线平行同旁内角互补得出∠2的度数. 如图是我国古代数学家杨辉最早发现的图形，称为“杨辉三角”．他的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如其中每一行的数字正好对应了（a＋b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，(a＋b)2＝a2＋2ab＋b2，展开式中的系数1、2、1恰好对应图中第三行的数字；再如，(a＋b)3＝a3＋3a2b＋3ab2＋b3，展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a＋b)4的展开式，(a＋b)4＝_______．
a4＋4a3b＋6a2b2＋4ab3＋b4
【解析】根据题意得：(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
故答案为：a4＋4a3b＋6a2b2＋4ab3＋b4 下列说法中正确的是（ ）
①角平分线上任意一点到角的两边的线段长相等 ②角是轴对称图形
③线段不是轴对称图形 ④矩形是轴对称图形
A. ①②③④ B. ①②③ C. ②④ D. ②③④
C
【解析】【解析】
①叙述不清，正确的应该是“角平分线上任意一点到角的两边的距离相等”；②正确，对称轴是角平分线所在直线；③错误，线段本身也是轴对称图形，有2条对称轴；④正确，非正方形的矩形有两条对称轴，正方形有四条对称轴．故选C．