题目内容
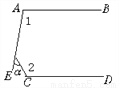
如图，已知AB∥CD，∠1=100°，∠2=120°，则∠α=_____.
40°
【解析】
延长AE、DC相交于点F.
∵AB∥CD，∠1=100°，
∴∠F=180°-100°=80°，
∴∠α=∠2-∠F=120°-80°=40°.
练习册系列答案
相关题目
如图,已知线段AB,BC的垂直平分线l1,l2交于点M,则线段AM,CM的大小关系是( )
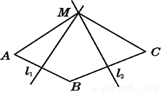
A. AM>CM B. AM=CM C. AM<CM D. 无法确定
B
【解析】首先连接BM，然后根据l1是线段AB的垂直平分线判定AM=BM；类似的方法可得BM与CM的关系，最后利用等量代换即可解答本题.
【解析】
如图所示：连接BM，
∵l1是线段AB的垂直平分线，
∴AM=BM，
∵l2是线段BC的垂直平分线，
∴BM=CM，
∴AM=CM.
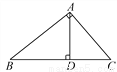
故选B. 如图，Rt△ABC中，∠A＝90°，AD⊥BC于点D，若BD∶CD＝3∶2，则tan∠B＝_____________．
,
【解析】∵BD：CD=3：2，∴不妨取BD=3，CD=2，
∵Rt△ABC中，∠A=90°，AD⊥BC于点D，∴AD2=BD•CD=6，解得AD＝，
∴tanB＝，
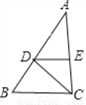
故答案为： ． 如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．
40°
【解析】试题分析：根据平行线的性质求出∠ACB的度数，根据角平分线定义求出即可.
试题解析：
∵ DE∥BC，∠AED =80°，∴ ∠EDC =∠BCD，∠ACB=∠AED=80°
∵ CD平分∠ACB，
∴ ∠BCD= ∠ACB=40°，∴ ∠EDC=∠BCD=40° 下列语句错误的是( )
A. 锐角的补角一定是钝角 B. 一个锐角和一个钝角一定互补
C. 互补的两角不能都是钝角 D. 互余且相等的两角都是45°
B
【解析】A. ∵锐角小于90°，∴ 锐角的补角一定是钝角，故正确；
B. ∵如：30°+100°=130°，∴一个锐角和一个钝角不一定互补，故不正确；
C. ∵如果两个角都是钝角，则其和就大于180°，∴互补的两角不能都是钝角，故正确；
D. ∵互余且相等的两角都是45°，故正确；
故选B. 如图，已知直线a∥b,c∥d，∠1=115°，则∠2=_____，∠3=_____.
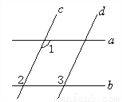
115° 115°
【解析】∵a∥b,∠1=115°，
∴∠2=∠1=115°.
∵c∥d，
∴∠3=∠2=115°. 已知：如图，A、B两点在直线l的同侧，点A'与A关于直线l对称，连接A'B交l于P点，若A'B＝a.
（1）求AP＋PB；
（2）若点M是直线l上异于P点的任意一点，求证：AM＋MB＞AP＋PB．
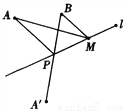
答案见解析
【解析】试题分析： 由轴对称的性质可知： 从而可求得答案；
由两点之间线段最短进行证明即可．
试题解析：(1)∵点A′与A关于直线l对称，
∴PA=PA′.
∴PA+PB=PA′+PB=A′B=a.
(2)∵点A′与A关于直线l对称，
∴MA=MA′.
∴AM+BM=MA′+MB.
由(1)可知：AP+PB=A′B
由两点之间线段... 已知a+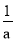
=5,则a2+
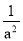的结果是___________.
23
【解析】由题意知=25,即a2++2=25,所以a2+=23. 下列图形中对称轴最多的是（ ）
A. 圆 B. 正方形 C. 角 D. 线段
A
【解析】试题分析：根据轴对称图形的对称轴的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．这条直线就是它的对称轴．
【解析】
A、圆的对称轴有无数条，它的每一条直径所在的直线都是它的对称轴；
B、正方形的对称轴有4条；
C、角的对称轴有1条；
D、线段的对称轴有2条．
故图形中对称轴最多的是圆．
故选A．
...