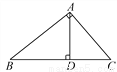
如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tan∠B=_____________.
 ,
,
 【解析】∵BD:CD=3:2,∴不妨取BD=3,CD=2,
∵Rt△ABC中,∠A=90°,AD⊥BC于点D,∴AD2=BD•CD=6,解得AD=,
∴tanB=,
故答案为: .
【解析】∵BD:CD=3:2,∴不妨取BD=3,CD=2,
∵Rt△ABC中,∠A=90°,AD⊥BC于点D,∴AD2=BD•CD=6,解得AD=,
∴tanB=,
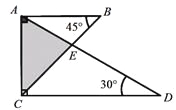
故答案为: . 将一副三角尺如图所示叠放在一起,则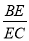 的值是 .
的值是 .
 【解析】试题分析:设AC=BC=x,则CD= ,证得AB∥CD,进而得△ABE∽△DCE,所以=.
故答案为: .
【解析】试题分析:设AC=BC=x,则CD= ,证得AB∥CD,进而得△ABE∽△DCE,所以=.
故答案为: . 在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.已知AE=5,tan∠AED=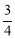 ,则BE+CE= .
,则BE+CE= .
 6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B...
6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B... 计算:
(1) 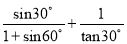 ;
;
(2)tan30°·tan60°+sin245°+cos245°.
 (1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=.
(1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=. 如图,在△ABC中,CD⊥AB,垂足为点D.若AB=12,CD=6,tanA=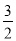 ,求sinB+cosB的值.
,求sinB+cosB的值.
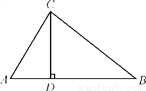
 .
【解析】试题分析:先在Rt△ACD中,由正切函数的定义得tanA==,求出AD=4,则BD=AB﹣AD=8,再解Rt△BCD,由勾股定理得BC==10,sinB==,cosB==,由此求出sinB+cosB=.
【解析】
在Rt△ACD中,∵∠ADC=90°,
∴tanA===,
∴AD=4,
∴BD=AB﹣AD=12﹣4=8.
在Rt△BCD中,∵∠BD...
.
【解析】试题分析:先在Rt△ACD中,由正切函数的定义得tanA==,求出AD=4,则BD=AB﹣AD=8,再解Rt△BCD,由勾股定理得BC==10,sinB==,cosB==,由此求出sinB+cosB=.
【解析】
在Rt△ACD中,∵∠ADC=90°,
∴tanA===,
∴AD=4,
∴BD=AB﹣AD=12﹣4=8.
在Rt△BCD中,∵∠BD... 如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
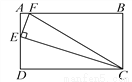
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
 (1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ...
(1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ... 阅读下面的材料,再回答问题:
三角函数中常用公式sin(A+B)=sinAcosB+cosAsinB,求sin(A+B)的值.
例如:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=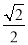 ×
×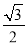 +
+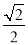 ×
×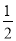 =
=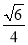 +
+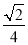 =
=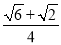 .
.
试用公式cos(A+B)=cosAcosB-sinAsinB,求cos75°的值.
 【解析】试题分析:将cos75°变为cos(45°+30°),然后按所给的公式进行计算即可.
试题解析:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=.
【解析】试题分析:将cos75°变为cos(45°+30°),然后按所给的公式进行计算即可.
试题解析:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=. 如图,直线y=2x+2与y轴交于A点,与反比例函数y=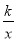 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
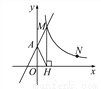
(1)求k的值;
(2)点N(a,1)是反比例函数y=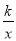 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
 (1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
(1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置. 超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.
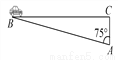
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732, 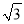 ≈1.732,60千米/小时≈16.7米/秒)
≈1.732,60千米/小时≈16.7米/秒)
 (1)112米;(2)没有超过限制速度.
【解析】【解析】
(1)在Rt△ABC中,
∠ACB=90°,∠BAC=75°,AC=30,
∴BC=AC·tan ∠BAC=30×tan 75°≈30×3.732≈112(米).
(2)∵此车速度=112÷8=14(米/秒)<16.7(米/秒)=60(千米/小时)
∴此车没有超过限制速度.
(1)112米;(2)没有超过限制速度.
【解析】【解析】
(1)在Rt△ABC中,
∠ACB=90°,∠BAC=75°,AC=30,
∴BC=AC·tan ∠BAC=30×tan 75°≈30×3.732≈112(米).
(2)∵此车速度=112÷8=14(米/秒)<16.7(米/秒)=60(千米/小时)
∴此车没有超过限制速度. 如图,在Rt△ABC中,∠C=90°,若sinA=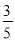 ,则cosB的是
,则cosB的是
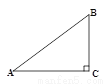
A. 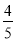 B.
B. 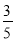 C.
C. 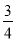 D.
D. 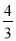
 B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B.
B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B.