题目内容
将一副三角尺如图所示叠放在一起,则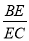 的值是 .
的值是 .
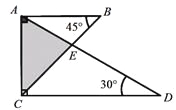
 【解析】试题分析:设AC=BC=x,则CD= ,证得AB∥CD,进而得△ABE∽△DCE,所以=.
故答案为: .
【解析】试题分析:设AC=BC=x,则CD= ,证得AB∥CD,进而得△ABE∽△DCE,所以=.
故答案为: .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案某校九年级(1)班50名学生中有20名团员,他们都积极报名参加学校开展的“文明劝导活动”。根据要求,该班从团员中随机抽取1名参加,则该班团员京京被抽到的概率是 【 】
A.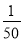 B.
B.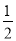 C.
C.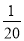 D.
D. 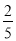
 C
【解析】【解析】
全部是20名团员,抽取1名,所以被抽到的概率是,故选C。
C
【解析】【解析】
全部是20名团员,抽取1名,所以被抽到的概率是,故选C。 如图,△ABC,△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌△CEB.
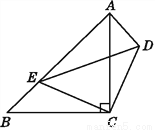
 答案见解析
【解析】试题分析:根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.
试题解析:证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中, ,
∴△CDA≌△CEB.
答案见解析
【解析】试题分析:根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.
试题解析:证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中, ,
∴△CDA≌△CEB. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
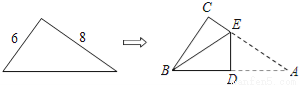
A. 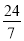 B.
B. 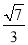 C.
C. 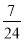 D.
D. 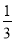
 C
【解析】试题分析:根据折叠变换的性质可知AE=BE,设CE=x,可知BE=8-x,根据勾股定理得,即,解得x=,因此可求tan∠CBE=.
故选C
C
【解析】试题分析:根据折叠变换的性质可知AE=BE,设CE=x,可知BE=8-x,根据勾股定理得,即,解得x=,因此可求tan∠CBE=.
故选C 阅读下面的材料,再回答问题:
三角函数中常用公式sin(A+B)=sinAcosB+cosAsinB,求sin(A+B)的值.
例如:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=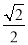 ×
×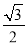 +
+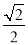 ×
×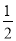 =
=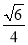 +
+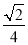 =
=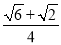 .
.
试用公式cos(A+B)=cosAcosB-sinAsinB,求cos75°的值.
 【解析】试题分析:将cos75°变为cos(45°+30°),然后按所给的公式进行计算即可.
试题解析:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=.
【解析】试题分析:将cos75°变为cos(45°+30°),然后按所给的公式进行计算即可.
试题解析:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=. 在Rt△ABC中,∠C=90°,下列说法正确的有( )
①sinA>cosA ②sin2A+cos2A=1 ③tanA·tanB=1 ④tanA=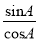
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
 B
【解析】∵∠C=90°,∴,已知中不知BC与AC在大小关系,故①错误;
,故②正确;
,故③正确;
,故④正确,
故选B.
B
【解析】∵∠C=90°,∴,已知中不知BC与AC在大小关系,故①错误;
,故②正确;
,故③正确;
,故④正确,
故选B. 阅读下面的证明过程,指出其错误.
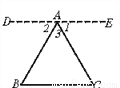
已知△ABC
求证:∠A+∠B+∠C=180°
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°
 答案见解析
【解析】试题分析:注意作辅助线的方法,过点A作的辅助线不能同时满足两个条件.只能作平行线后,根据平行线的性质得到∠1=∠C.
错误①:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.
错误②:∵∠1=∠C(画图),理由错,应改为:两直线平行,内错角相等.
答案见解析
【解析】试题分析:注意作辅助线的方法,过点A作的辅助线不能同时满足两个条件.只能作平行线后,根据平行线的性质得到∠1=∠C.
错误①:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.
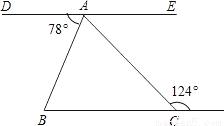
错误②:∵∠1=∠C(画图),理由错,应改为:两直线平行,内错角相等. 如图,DAE是一条直线,DE∥BC,则∠BAC=___度.
 46°.
【解析】试题分析:∵DE∥BC,∴∠DAC=124°,∴∠BAC=∠DAC﹣∠DAB=124°﹣78°=46°.故答案为:46°.
46°.
【解析】试题分析:∵DE∥BC,∴∠DAC=124°,∴∠BAC=∠DAC﹣∠DAB=124°﹣78°=46°.故答案为:46°. 如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为( )

A. (2a2+5a)cm2 B. (6a+15)cm2
C. (6a+9)cm2 D. (3a+15)cm2
 B
【解析】由题意可得,(a+4)2-(a+1)2=a2+8a+16-(a2+2a+1)=a2+8a+16-a2-2a-1=6a+15(cm2),故选B.
B
【解析】由题意可得,(a+4)2-(a+1)2=a2+8a+16-(a2+2a+1)=a2+8a+16-a2-2a-1=6a+15(cm2),故选B. 
