题目内容
计算:
(1) 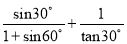 ;
;
(2)tan30°·tan60°+sin245°+cos245°.
 (1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=.
(1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案在相同条件下重复试验,若事件A发生的概率是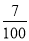 ,下列陈述中,正确的是( )
,下列陈述中,正确的是( )
A. 事件A发生的频率是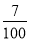
B. 反复大量做这种试验,事件A只发生了7次
C. 做100次这种试验,事件A一定发生7次
D. 做100次这种试验,事件A可能发生7次
 D
【解析】试题分析:∵事件A发生的概率是,不表示事件A发生的频率是,
∴选项A不正确;∵事件A发生的概率是,不表示事件A只发生了7次,可能比7次多,也有可能比7次少,
∴选项B不正确;
∵事件A发生的概率是,不表示事件A一定发生7次,
∴选项C不正确;
∵事件A发生的概率是,表示事件A可能发生7次,
∴选项D正确.
故选D.
D
【解析】试题分析:∵事件A发生的概率是,不表示事件A发生的频率是,
∴选项A不正确;∵事件A发生的概率是,不表示事件A只发生了7次,可能比7次多,也有可能比7次少,
∴选项B不正确;
∵事件A发生的概率是,不表示事件A一定发生7次,
∴选项C不正确;
∵事件A发生的概率是,表示事件A可能发生7次,
∴选项D正确.
故选D. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
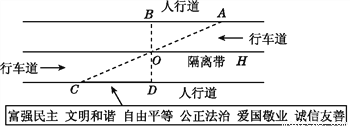
 20米.
【解析】试题分析:已知AB∥CD,根据平行线的性质可得∠ABO=∠CDO,再由垂直的定义可得∠CDO=90°,可得OB⊥AB,根据相邻两平行线间的距离相等可得OD=OB,即可根据ASA定理判定△ABO≌△CDO,由全等三角形的性质即可得CD=AB=20m.
试题解析:∵AB∥CD,∴∠ABO=∠CDO,
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即O...
20米.
【解析】试题分析:已知AB∥CD,根据平行线的性质可得∠ABO=∠CDO,再由垂直的定义可得∠CDO=90°,可得OB⊥AB,根据相邻两平行线间的距离相等可得OD=OB,即可根据ASA定理判定△ABO≌△CDO,由全等三角形的性质即可得CD=AB=20m.
试题解析:∵AB∥CD,∴∠ABO=∠CDO,
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即O... 如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则cosC的值为_______.
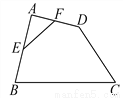
 【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: .
【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: . 超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.
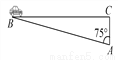
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732, 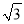 ≈1.732,60千米/小时≈16.7米/秒)
≈1.732,60千米/小时≈16.7米/秒)
 (1)112米;(2)没有超过限制速度.
【解析】【解析】
(1)在Rt△ABC中,
∠ACB=90°,∠BAC=75°,AC=30,
∴BC=AC·tan ∠BAC=30×tan 75°≈30×3.732≈112(米).
(2)∵此车速度=112÷8=14(米/秒)<16.7(米/秒)=60(千米/小时)
∴此车没有超过限制速度.
(1)112米;(2)没有超过限制速度.
【解析】【解析】
(1)在Rt△ABC中,
∠ACB=90°,∠BAC=75°,AC=30,
∴BC=AC·tan ∠BAC=30×tan 75°≈30×3.732≈112(米).
(2)∵此车速度=112÷8=14(米/秒)<16.7(米/秒)=60(千米/小时)
∴此车没有超过限制速度. 在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=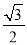 ;②cosB=
;②cosB=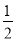 ;③tanA=
;③tanA=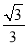 ;④tanB=
;④tanB=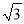 ,其中正确的结论是_____ .
,其中正确的结论是_____ .
 ②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。
②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。 在Rt△ABC中,∠C=90°,sinA=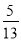 ,则tanA的值为( )
,则tanA的值为( )
A. 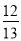 B.
B. 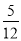 C.
C. 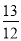 D.
D. 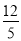
 B
【解析】在△ABC中,∵∠C=90°,∴,又,∴,设BC=5k(k≠0),则AB=13k,∴,∴,故选D.
B
【解析】在△ABC中,∵∠C=90°,∴,又,∴,设BC=5k(k≠0),则AB=13k,∴,∴,故选D. 如图,标有角号的7个角中共有________对内错角,________对同位角,________对同旁内角.
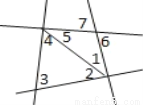
 4对 2对 4对
【解析】【解析】
如图,共有4对内错角:分别是∠1和∠4,∠2和∠5,∠6和∠1,∠5和∠7;
2对同位角:分别是∠7和∠1,∠5和∠6;
4对同旁内角:分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2.
4对 2对 4对
【解析】【解析】
如图,共有4对内错角:分别是∠1和∠4,∠2和∠5,∠6和∠1,∠5和∠7;
2对同位角:分别是∠7和∠1,∠5和∠6;
4对同旁内角:分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2. 若9x2+kxy+16y2是完全平方式,则k的值为( )
A. 12 B. 24 C. ±12 D. ±24
 D
【解析】已知9x2+kxy+16y2是完全平方式,可得kxy=±2×3x•4y,解得k=±24.故选D.
D
【解析】已知9x2+kxy+16y2是完全平方式,可得kxy=±2×3x•4y,解得k=±24.故选D. 
