题目内容
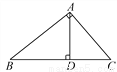
如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tan∠B=_____________.
 ,
,
 【解析】∵BD:CD=3:2,∴不妨取BD=3,CD=2,
∵Rt△ABC中,∠A=90°,AD⊥BC于点D,∴AD2=BD•CD=6,解得AD=,
∴tanB=,
故答案为: .
【解析】∵BD:CD=3:2,∴不妨取BD=3,CD=2,
∵Rt△ABC中,∠A=90°,AD⊥BC于点D,∴AD2=BD•CD=6,解得AD=,
∴tanB=,
故答案为: .
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知粉笔盒里只有2支红色粉笔和3支白色粉笔,每支粉笔除颜色外其他均相同,现从中任取一支粉笔,则取出白色粉笔的概率是( )
A. 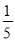 B.
B. 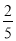 C.
C. 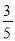 D.
D. 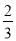
 C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C.
C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C. 如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 ________度.

 110
【解析】∵∠ABC=∠ADC=90°,CB=CD,且CA=CA,
∴△ABC≌△ADC,
∴∠BCA=∠DCA,
∵∠BAC=35°,∠ABC=90°,
∴∠BCA=55°,
∴∠BCD=2∠BCA=110°,
故答案为:110.
110
【解析】∵∠ABC=∠ADC=90°,CB=CD,且CA=CA,
∴△ABC≌△ADC,
∴∠BCA=∠DCA,
∵∠BAC=35°,∠ABC=90°,
∴∠BCA=55°,
∴∠BCD=2∠BCA=110°,
故答案为:110. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=4,BC=6,则tan∠ACD的值为( )
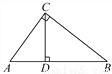
A. 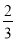 B.
B. 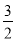 C.
C. 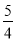 D.
D. 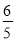
 A
【解析】∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ADC=90°,∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵tanB =,
∴tan∠ACD =,
故选A.
A
【解析】∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ADC=90°,∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵tanB =,
∴tan∠ACD =,
故选A. 如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
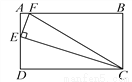
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
 (1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ...
(1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ... 一斜坡的坡度为1∶3,如果某人站的位置的水平宽度为6米,则他所在的位置的铅直高度为( )
A. 2米 B. 18米 C. 3米 D. 6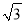 米
米
 A
【解析】设他所在的位置的铅直高度为x米,由题意得
x:6=1:3,
解得:x=2,
故选A.
A
【解析】设他所在的位置的铅直高度为x米,由题意得
x:6=1:3,
解得:x=2,
故选A. 根据下列证明过程填空:
如图,已知BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C
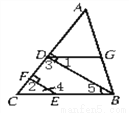
证明:∵BD⊥AC,EF⊥AC
∴∠2=∠3=90°( )
∴BD∥EF ( )
∴∠4=_____( )
∵∠1=∠4
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
 见解析
【解析】试题分析:解决问题要熟悉平行线的性质和判定,能正确运用语言叙述理由,还要注意平行线的性质和判定的综合运用.
试题解析:∵BD⊥AC,EF⊥AC(已知),
∴∠2=∠3=90°,
∴BD∥EF(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,同位角相等);
∵∠1=∠4(已知),
∴∠1=∠5(等量代换),
∴DG∥BC(内错角相...
见解析
【解析】试题分析:解决问题要熟悉平行线的性质和判定,能正确运用语言叙述理由,还要注意平行线的性质和判定的综合运用.
试题解析:∵BD⊥AC,EF⊥AC(已知),
∴∠2=∠3=90°,
∴BD∥EF(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,同位角相等);
∵∠1=∠4(已知),
∴∠1=∠5(等量代换),
∴DG∥BC(内错角相... 如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α=_____.
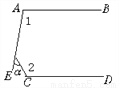
 40°
【解析】
延长AE、DC相交于点F.
∵AB∥CD,∠1=100°,
∴∠F=180°-100°=80°,
∴∠α=∠2-∠F=120°-80°=40°.
40°
【解析】
延长AE、DC相交于点F.
∵AB∥CD,∠1=100°,
∴∠F=180°-100°=80°,
∴∠α=∠2-∠F=120°-80°=40°. 如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为 ( )
A. –3 B. 3 C. 0 D. 1
 A
【解析】(x+m)(x+3)=x2+(3+m)x+3m,
因为结果不含x的一次项,所以3+m=0,m=-3,
故选A.
A
【解析】(x+m)(x+3)=x2+(3+m)x+3m,
因为结果不含x的一次项,所以3+m=0,m=-3,
故选A. 
