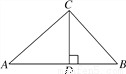
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=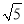 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A. 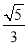 B.
B. 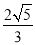 C.
C. 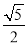 D.
D. 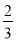
 A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A. 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=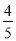 ,则下列结论中正确的个数为( )
,则下列结论中正确的个数为( )
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
.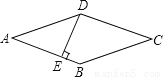
A.3个 B.2个 C.1个 D.0个
 A.
【解析】
试题解析:由题意可得,菱形的边长为5cm,又cosA=,所以AE=4,
则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2,
故选A.
A.
【解析】
试题解析:由题意可得,菱形的边长为5cm,又cosA=,所以AE=4,
则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2,
故选A. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=4,BC=6,则tan∠ACD的值为( )
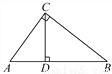
A. 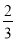 B.
B. 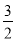 C.
C. 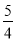 D.
D. 
 A
【解析】∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ADC=90°,∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵tanB =,
∴tan∠ACD =,
故选A.
A
【解析】∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ADC=90°,∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵tanB =,
∴tan∠ACD =,
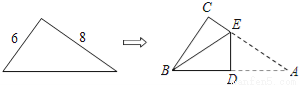
故选A. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. 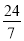 B.
B. 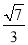 C.
C. 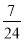 D.
D. 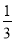
 C
【解析】试题分析:根据折叠变换的性质可知AE=BE,设CE=x,可知BE=8-x,根据勾股定理得,即,解得x=,因此可求tan∠CBE=.
故选C
C
【解析】试题分析:根据折叠变换的性质可知AE=BE,设CE=x,可知BE=8-x,根据勾股定理得,即,解得x=,因此可求tan∠CBE=.
故选C 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_.
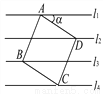
 【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵...
【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵... 如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则cosC的值为_______.
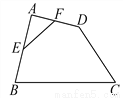
 【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: .
【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: . 如图,将以A为直角顶点的等腰Rt△ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则sin∠A′BC′的值为_____,cos∠A′BC=________.
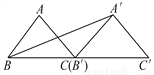
 【解析】过A′作出A′D⊥BC′,垂足为D,
在等腰直角三角形A′B′C′中,则A′D是底边上的中线,
∴B′C′=2 A′D,
∵BC=B′C′,BD=BC+B′D,
∴A′B= ,
∴ sin∠A′BC′=,cos∠A′BC=,
故答案为: , .
【解析】过A′作出A′D⊥BC′,垂足为D,
在等腰直角三角形A′B′C′中,则A′D是底边上的中线,
∴B′C′=2 A′D,
∵BC=B′C′,BD=BC+B′D,
∴A′B= ,
∴ sin∠A′BC′=,cos∠A′BC=,
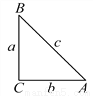
故答案为: , . 如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=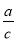 ,cosA=
,cosA=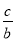 ,tanA=
,tanA=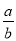 .我们不难发现:sin260°+cos260°=1,…,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
 sin2A+cos2A=1,tanA=,理由见解析.
【解析】试题分析:sin2A+cos2A=1,tanA=,根据三角函数的定义以及勾股定理通过推导即可得.
试题解析:sin2A+cos2A=1,tanA=,理由如下:
∵∠C=90°,∴a2+b2=c2,sinA=,cosA=,tanA=,
∴sin2A+cos2A=;
tanA=..
sin2A+cos2A=1,tanA=,理由见解析.
【解析】试题分析:sin2A+cos2A=1,tanA=,根据三角函数的定义以及勾股定理通过推导即可得.
试题解析:sin2A+cos2A=1,tanA=,理由如下:
∵∠C=90°,∴a2+b2=c2,sinA=,cosA=,tanA=,
∴sin2A+cos2A=;
tanA=.. 在△ABC中,∠C=90°,cosA=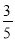 ,AC=6.求△ABC的周长和面积.
,AC=6.求△ABC的周长和面积.
 周长为24,面积为24.
【解析】试题分析:根据余弦的定义求出斜边AB的长,再根据勾股定理求出BC的长,再根据三角形的周长、面积的求法即可得.
试题解析:∵∠C=90°,∴cosA=,
∵cosA=,AC=6,
∴AB=10,
∴BC==8,
∴△ABC的周长=AC+BC+AB=6+8+10=24,
S△ABC==24.
周长为24,面积为24.
【解析】试题分析:根据余弦的定义求出斜边AB的长,再根据勾股定理求出BC的长,再根据三角形的周长、面积的求法即可得.
试题解析:∵∠C=90°,∴cosA=,
∵cosA=,AC=6,
∴AB=10,
∴BC==8,
∴△ABC的周长=AC+BC+AB=6+8+10=24,
S△ABC==24. 如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=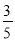 . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
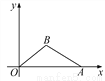
 (1)点B的坐标为(4,3);(2)cos∠BAO=.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足...
(1)点B的坐标为(4,3);(2)cos∠BAO=.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足...