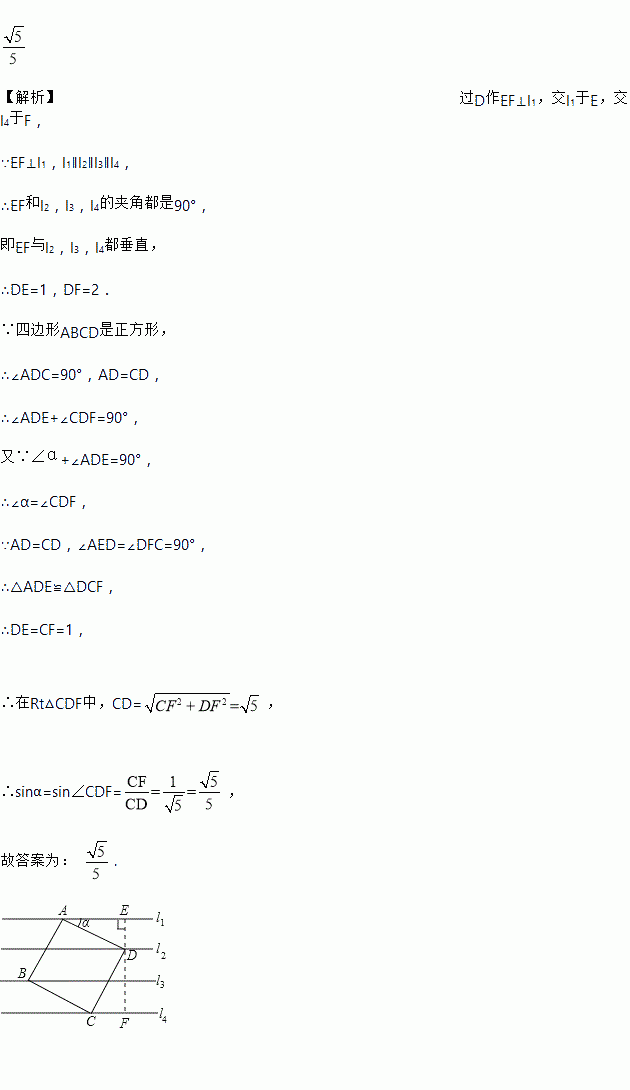题目内容
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_.
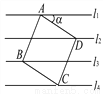
 【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵...
【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵...
练习册系列答案
相关题目
一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,将球搅匀,从中任意摸出1个球.
(1)会出现哪些可能的结果? ;
(2)你认为摸到哪种颜色球的可能性最大? ;
(3)怎样改变袋子中红球和白球的个数,使摸到这两种颜色球的概率相同?
 (1)摸到红球,摸到绿球,摸到白球;(2)白球(3)放入3个红球;放入2个红球,拿走1个白球等
【解析】
试题分析:(1)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可求得答案;
(2)由一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,即可求得摸到各种颜色球的概率,继而求得答案;
(3)使得袋子中红球和白球的个数相等即可.
【解析】
...
(1)摸到红球,摸到绿球,摸到白球;(2)白球(3)放入3个红球;放入2个红球,拿走1个白球等
【解析】
试题分析:(1)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可求得答案;
(2)由一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,即可求得摸到各种颜色球的概率,继而求得答案;
(3)使得袋子中红球和白球的个数相等即可.
【解析】
... 如图,MP,NQ分别垂直平分AB,AC,且BC=6 cm,则△APQ的周长为( )
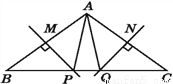
A. 12 cm B. 6 cm C. 8 cm D. 无法确定
 B
【解析】由MP、NQ分别垂直平分AB、AC,根据线段垂直平分线的性质,可得BP=AP,CQ=AQ,继而求得△APQ的周长等于BC.
【解析】
∵MP、NQ分别垂直平分AB、AC,
∴BP=AP,CQ=AQ,
∵BC=6cm,
∴△APQ的周长为:AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B.
B
【解析】由MP、NQ分别垂直平分AB、AC,根据线段垂直平分线的性质,可得BP=AP,CQ=AQ,继而求得△APQ的周长等于BC.
【解析】
∵MP、NQ分别垂直平分AB、AC,
∴BP=AP,CQ=AQ,
∵BC=6cm,
∴△APQ的周长为:AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B. 如图,有一个直角△ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P.Q两点分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,才能使ΔABC≌ΔPQA.
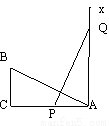
 10
【解析】
试题分析:要使△ABC≌△PQA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAQ=90°,
又∵AP=CB=5,PQ=AB,
∴△ABC≌△PQA.
点P运动到C点时,△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
...
10
【解析】
试题分析:要使△ABC≌△PQA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAQ=90°,
又∵AP=CB=5,PQ=AB,
∴△ABC≌△PQA.
点P运动到C点时,△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
... 如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=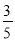 . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
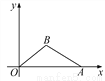
 (1)点B的坐标为(4,3);(2)cos∠BAO=.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足...
(1)点B的坐标为(4,3);(2)cos∠BAO=.
【解析】试题分析:(1)作BH⊥OA, 垂足为H,在Rt△OHB中,根据锐角三角函数的定义及已知条件求得BH的长,再根据勾股定理求得OH的长,即可得点B的坐标;(2)先求得AH的长,在Rt△AHB中,根据勾股定理求得AB的长,根据锐角三角函数的定义即可求得cos∠BAO的值.
试题解析:
(1)如图所示,作BH⊥OA, 垂足... 如图,在Rt△ABC中,∠C=90°,若sinA=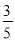 ,则cosB的是
,则cosB的是
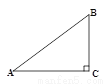
A. 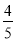 B.
B. 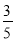 C.
C. 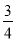 D.
D. 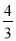
 B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B.
B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B. 在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.已知AE=5,tan∠AED=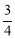 ,则BE+CE= .
,则BE+CE= .
 6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B...
6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
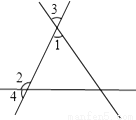
②若∠BAC为钝角,如答图2所示,同理可求得:B... ∠1=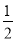 ∠2,∠1+∠2=162°,求∠3与∠4的度数.
∠2,∠1+∠2=162°,求∠3与∠4的度数.
 ∠3=54°,∠4=72°
【解析】试题分析:先由∠1=∠2,∠1+∠2=162°,求出∠1和∠2的度数;再根据∠1和∠3 是对顶角,∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2,∠1+∠2=162°,
∴∠1=54°, ∠2=108°.
∵∠1和∠3是对顶角,
∴∠3=∠1=54°
∵∠2和∠4是邻补角,
∴∠4=180°-∠2=180°-10...
∠3=54°,∠4=72°
【解析】试题分析:先由∠1=∠2,∠1+∠2=162°,求出∠1和∠2的度数;再根据∠1和∠3 是对顶角,∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2,∠1+∠2=162°,
∴∠1=54°, ∠2=108°.
∵∠1和∠3是对顶角,
∴∠3=∠1=54°
∵∠2和∠4是邻补角,
∴∠4=180°-∠2=180°-10... 先化简,再求值:-(a2-2ab)·9a2-(9ab3+12a4b2)÷3ab,其中a=-1,b=2.
 -49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49.
-49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49.