题目内容
如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则cosC的值为_______.
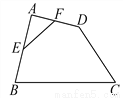
 【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: .
【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: .
 阅读快车系列答案
阅读快车系列答案暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
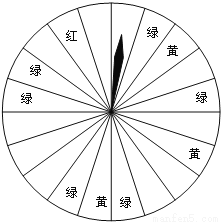
(1)求他此时获得购物券的概率是多少?
(2)他获得哪种购物券的概率最大?请说明理由.
 (1);(2)获得50元购物券的概率最大.
【解析】
试题分析:(1)由转盘被均匀地分为20份,他此时获得购物券的有10份,直接利用概率公式求解即可求得答案;
(2)分别求得获得200元、100元、50元的购物券的概率,即可求得答案.
【解析】
(1)∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是:=;
(2)∵P(获得20...
(1);(2)获得50元购物券的概率最大.
【解析】
试题分析:(1)由转盘被均匀地分为20份,他此时获得购物券的有10份,直接利用概率公式求解即可求得答案;
(2)分别求得获得200元、100元、50元的购物券的概率,即可求得答案.
【解析】
(1)∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是:=;
(2)∵P(获得20... 如图,已知直线l是AB的垂直平分线,M是直线l上的一点,D,E是AB上不同的点,则AM=BM吗?MD=ME吗?
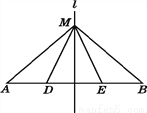
 AM=BM,无法判断MD是否等于ME.
【解析】由M在线段AB的垂直平分线l上,根据“线段的垂直平分线上任意一点,到线段两端点的距离相等”即可判断AM=BM成立;根据直线l不一定是DE的垂直平分线,则无法判断MD与ME的大小关系.
【解析】
∵l是AB的垂直平分线,
∴AM=BM.
由于D、E是AB上任意两点,所以MD不一定等于ME,只有当l经过DE的中点时,MD=ME....
AM=BM,无法判断MD是否等于ME.
【解析】由M在线段AB的垂直平分线l上,根据“线段的垂直平分线上任意一点,到线段两端点的距离相等”即可判断AM=BM成立;根据直线l不一定是DE的垂直平分线,则无法判断MD与ME的大小关系.
【解析】
∵l是AB的垂直平分线,
∴AM=BM.
由于D、E是AB上任意两点,所以MD不一定等于ME,只有当l经过DE的中点时,MD=ME.... 如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是( )

A. AB=A′B′=5,BC=B′C′=3 B. AB=B′C′=5,∠A=∠B′=40°
C. AC=A′C′=5,BC=B′C′=3 D. AC=A′C′=5,∠A=∠A′=40°
 B
【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°
A选项:AB=A′B′=5,BC=B′C′=3,
符合直角三角形全等的判定条件HL,
∴A选项能使Rt△ABC≌Rt△A′B′C′;
B选项:AB=B′C′=5,∠A=∠B′=40°,
不符合符合直角三角形全等的判定条件,
∴B选项不能使Rt△ABC≌Rt△A′B′C′;
C选项符合Rt△ABC和Rt△A...
B
【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°
A选项:AB=A′B′=5,BC=B′C′=3,
符合直角三角形全等的判定条件HL,
∴A选项能使Rt△ABC≌Rt△A′B′C′;
B选项:AB=B′C′=5,∠A=∠B′=40°,
不符合符合直角三角形全等的判定条件,
∴B选项不能使Rt△ABC≌Rt△A′B′C′;
C选项符合Rt△ABC和Rt△A... 如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA= .
.
(1)求线段CD的长;
(2)求sin∠DBE的值.
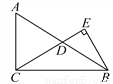
 (1)CD=;(2)sin∠DBE=.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长;(2)由于D为AB上的中点,求出AD=BD=CD=,设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可.
试题解析::【解析】
(1)∵AC=15,cosA=,
∴cosA=,
∴AB=25,
∵△ACB为直角三角形,...
(1)CD=;(2)sin∠DBE=.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长;(2)由于D为AB上的中点,求出AD=BD=CD=,设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可.
试题解析::【解析】
(1)∵AC=15,cosA=,
∴cosA=,
∴AB=25,
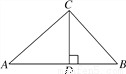
∵△ACB为直角三角形,... 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=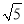 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A. 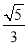 B.
B. 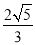 C.
C. 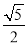 D.
D. 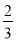
 A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A. 计算:
(1) 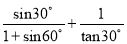 ;
;
(2)tan30°·tan60°+sin245°+cos245°.
 (1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=.
(1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
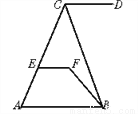
(2)原式=. 如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
 平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥...
平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥... (1) 已知a+b=7,ab=12.求下列各式的值:
①a2-ab+b2;②(a-b)2.
(2)已知a=275,b=450,c=826,d=1615,比较a,b,c,d的大小.
 (1) ①3;②1; (2)b>c>a>d.
【解析】试题分析:(1)①将a2-ab+b2化为(a+b)2-3ab,再代入求值即可;②将(a-b)2化为(a+b)2-4ab,再代入求值即可;(2)将a=275,b=450,c=826,d=1615都化为底数为2的幂,再比较大小即可.
试题解析:
(1) ①a2-ab+b2=a2+b2-ab=(a+b)2-3ab=72-3×12=1...
(1) ①3;②1; (2)b>c>a>d.
【解析】试题分析:(1)①将a2-ab+b2化为(a+b)2-3ab,再代入求值即可;②将(a-b)2化为(a+b)2-4ab,再代入求值即可;(2)将a=275,b=450,c=826,d=1615都化为底数为2的幂,再比较大小即可.
试题解析:
(1) ①a2-ab+b2=a2+b2-ab=(a+b)2-3ab=72-3×12=1... 
