题目内容
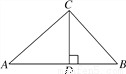
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=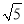 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A. 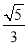 B.
B. 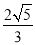 C.
C. 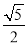 D.
D. 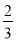
 A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从分别标有1、2、3、4的四张卡片中,一次同时抽2张,其中和为奇数的概率是 .
 【解析】试题分析:如图所示,
由树状图可知共有4×3=12种可能,和为奇数的有8种,所以概率是=.故答案为: .
【解析】试题分析:如图所示,
由树状图可知共有4×3=12种可能,和为奇数的有8种,所以概率是=.故答案为: . 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
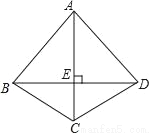
A. AB=AD B. AC平分∠BCD C. AB=BD D. △BEC≌△DEC
 C
【解析】试题分析:根据AC垂直平分BD可得:△ABD为等腰三角形,即AB=AD,AC平分∠BAD,△BEC≌△DEC.
C
【解析】试题分析:根据AC垂直平分BD可得:△ABD为等腰三角形,即AB=AD,AC平分∠BAD,△BEC≌△DEC. 如图,∠C=∠D=90°,若添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,则以下给出的条件适合的是( )
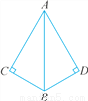
A. AC=AD B. AB=AB C. ∠ABC=∠ABD D. ∠BAC=∠BAD
 A
【解析】根据题意可知∠C=∠D=90°,AB=AB,
然后由AC=AD,可根据HL判定两直角三角形全等,故符合条件;
而B答案只知道一边一角,不能够判定两三角形全等,故不正确;
C答案符合AAS,证明两三角形全等,故不正确;
D答案是符合AAS,能证明两三角形全等,故不正确.
故选:A.
A
【解析】根据题意可知∠C=∠D=90°,AB=AB,
然后由AC=AD,可根据HL判定两直角三角形全等,故符合条件;
而B答案只知道一边一角,不能够判定两三角形全等,故不正确;
C答案符合AAS,证明两三角形全等,故不正确;
D答案是符合AAS,能证明两三角形全等,故不正确.
故选:A. 如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则cosC的值为_______.
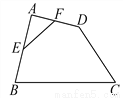
 【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: .
【解析】连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且BD=2EF=4,
∵BD=4,BC=5,CD=3,
∴△BDC是直角三角形,
∴tan C=,
故答案为: . 如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
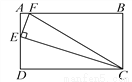
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
 (1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ...
(1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ... 在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=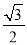 ;②cosB=
;②cosB=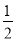 ;③tanA=
;③tanA=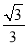 ;④tanB=
;④tanB=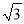 ,其中正确的结论是_____ .
,其中正确的结论是_____ .
 ②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。
②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。 如图,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD等于( )
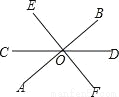
A. 40° B. 45° C. 55° D. 65°
 A
【解析】∵EF⊥AB于O,∠COE=50°,
∴∠AOC=90°-50°=40°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=40°;
故选A。
A
【解析】∵EF⊥AB于O,∠COE=50°,
∴∠AOC=90°-50°=40°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=40°;
故选A。 已知x2-x-1=0,则代数式-x3+2x2+2 015的值为___________.
 2016
【解析】由已知得x2-x=1,所以-x3+2x2+2 015=-x(x2-x)+x2+2 015=-x+x2+2 015=2 016.
2016
【解析】由已知得x2-x=1,所以-x3+2x2+2 015=-x(x2-x)+x2+2 015=-x+x2+2 015=2 016.