��Ŀ����
��ͼ����Rt��ABC�У�BC��AC��AB���ߵij��ֱ�Ϊa��b��c����sinA��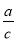 ��cosA��
��cosA��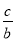 ��tanA��
��tanA��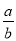 .���Dz��ѷ��֣�sin260�㣫cos260�㣽1��������̽��sinA��cosA��tanA֮����ڵ�һ���ϵ����˵�����ɣ�
.���Dz��ѷ��֣�sin260�㣫cos260�㣽1��������̽��sinA��cosA��tanA֮����ڵ�һ���ϵ����˵�����ɣ�
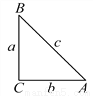
 sin2A��cos2A��1��tanA�������ɼ�����.
�����������������sin2A��cos2A��1��tanA�����������Ǻ����Ķ����Լ����ɶ���ͨ���Ƶ����ɵ�.
���������sin2A��cos2A��1��tanA�����������£�
�ߡ�C=90�㣬��a2+b2=c2��sinA����cosA����tanA����
��sin2A+cos2A����
tanA��..
sin2A��cos2A��1��tanA�������ɼ�����.
�����������������sin2A��cos2A��1��tanA�����������Ǻ����Ķ����Լ����ɶ���ͨ���Ƶ����ɵ�.
���������sin2A��cos2A��1��tanA�����������£�
�ߡ�C=90�㣬��a2+b2=c2��sinA����cosA����tanA����
��sin2A+cos2A����
tanA��..
һ������װ��2������3������5������ÿ��������ɫ�ⶼ��ͬ��������������һ���ֱ����������������ĸ��ʡ�
 ����
��������
������������������ܸ��������ݸ��ʵĶ���ֱ�Ӽ��㼴�ɣ�����=������������������֮�ȣ�
�����������������ĸ���Ϊ������������ĸ���Ϊ
��������ĸ���Ϊ����
����
��������
������������������ܸ��������ݸ��ʵĶ���ֱ�Ӽ��㼴�ɣ�����=������������������֮�ȣ�
�����������������ĸ���Ϊ������������ĸ���Ϊ
��������ĸ���Ϊ���� ��ͼ,��֪��PΪ��MON��һ��,��P���A����ֱ��ON�Գ�,��P���B����ֱ��OM�Գ�.����AB,��ON��D��,��OM��C��,��AB��Ϊ15 cm,���PCD���ܳ�.
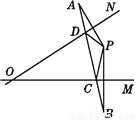
 15 cm.
���������ɵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƿɵã�ON��ֱƽ��AP��OM��ֱƽ��BP�����ݴ�ֱƽ���ߵ����ʿɵ�DA=DP��CP=CB��ͨ�����������õ���PCD���ܳ���AB��������ϵ���������.
��������
�ߵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƣ�
��ON��ֱƽ��AP��OM��ֱƽ��BP��
��DA=DP��CP=CB��
��...
15 cm.
���������ɵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƿɵã�ON��ֱƽ��AP��OM��ֱƽ��BP�����ݴ�ֱƽ���ߵ����ʿɵ�DA=DP��CP=CB��ͨ�����������õ���PCD���ܳ���AB��������ϵ���������.
��������
�ߵ�P���A����ֱ��ON�Գƣ���P���B����ֱ��OM�Գƣ�
��ON��ֱƽ��AP��OM��ֱƽ��BP��
��DA=DP��CP=CB��
��... ��ͼ��ʾ�����ı���ABCD�У�CB=CD����ABC=��ADC=90�㣬��BAC=35�㣬���BCD�Ķ���Ϊ ________�ȣ�

 110
���������ߡ�ABC=��ADC=90�㣬CB=CD����CA=CA��
���ABC�ա�ADC��
���BCA=��DCA��
�ߡ�BAC=35�㣬��ABC=90�㣬
���BCA=55�㣬
���BCD=2��BCA=110�㣬
�ʴ�Ϊ��110��
110
���������ߡ�ABC=��ADC=90�㣬CB=CD����CA=CA��
���ABC�ա�ADC��
���BCA=��DCA��
�ߡ�BAC=35�㣬��ABC=90�㣬
���BCA=55�㣬
���BCD=2��BCA=110�㣬
�ʴ�Ϊ��110�� ��ͼ����C����D��90�㣬������һ����������ʹ�á�HL���ж�Rt��ABC��Rt��ABDȫ�ȣ������¸����������ʺϵ���( )
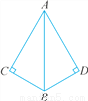
A. AC��AD B. AB��AB C. ��ABC����ABD D. ��BAC����BAD
 A
�����������������֪��C=��D=90�㣬AB=AB��
Ȼ����AC=AD���ɸ���HL�ж���ֱ��������ȫ�ȣ��ʷ���������
��B��ֻ֪��һ��һ�ǣ����ܹ��ж���������ȫ�ȣ��ʲ���ȷ��
C�𰸷���AAS��֤����������ȫ�ȣ��ʲ���ȷ��
D���Ƿ���AAS����֤����������ȫ�ȣ��ʲ���ȷ.
��ѡ��A.
A
�����������������֪��C=��D=90�㣬AB=AB��
Ȼ����AC=AD���ɸ���HL�ж���ֱ��������ȫ�ȣ��ʷ���������
��B��ֻ֪��һ��һ�ǣ����ܹ��ж���������ȫ�ȣ��ʲ���ȷ��
C�𰸷���AAS��֤����������ȫ�ȣ��ʲ���ȷ��
D���Ƿ���AAS����֤����������ȫ�ȣ��ʲ���ȷ.
��ѡ��A. ��ͼ����Rt��ABC�У���ACB��90�㣬CD��AB��D��AC��4��BC��6����tan��ACD��ֵΪ( )
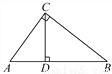
A. 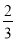 B.
B. 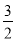 C.
C. 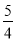 D.
D. 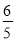
 A
���������ߡ�ACB=90�㣬���A+��B=90�㣬
�ߡ�ADC=90�㣬���A+��ACD=90�㣬
���ACD=��B��
��tanB =��
��tan��ACD =��
��ѡA.
A
���������ߡ�ACB=90�㣬���A+��B=90�㣬
�ߡ�ADC=90�㣬���A+��ACD=90�㣬
���ACD=��B��
��tanB =��
��tan��ACD =��
��ѡA. ��ͼ������ABCD�У�AB��2AD��EΪAD���е㣬EF��EC��AB�ڵ�F������FC.
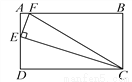
(1)��֤����AEF�ס�DCE��
(2)��tan��ECF��ֵ��
 ��1���𰸼���������2��
����������1�����ݾ��ε����ʿ�֪��A="��D" =90�㣬�ٸ��������ε��ڽǺ�Ϊ180�㣬��֪��DCE+��DEC=900������֪EF��EC���ɵã���AEF+��DEC=900�ó���DCE=��AEF������֤���SAEF�רSDCE
��2���ɣ�1����֪���SAEF�רSDCE ��=
�ھ���ABCD�У�EΪAD ���е㡣
AB=2AD �� DC=AB=4AE �� ...
��1���𰸼���������2��
����������1�����ݾ��ε����ʿ�֪��A="��D" =90�㣬�ٸ��������ε��ڽǺ�Ϊ180�㣬��֪��DCE+��DEC=900������֪EF��EC���ɵã���AEF+��DEC=900�ó���DCE=��AEF������֤���SAEF�רSDCE
��2���ɣ�1����֪���SAEF�רSDCE ��=
�ھ���ABCD�У�EΪAD ���е㡣
AB=2AD �� DC=AB=4AE �� ... ��������֤��������գ�
��ͼ����֪BD��AC��EF��AC��D��F�ֱ�Ϊ���㣬�ҡ�1=��4����֤����ADG=��C
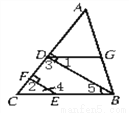
֤������BD��AC��EF��AC
���2=��3=90�㣨 ��
��BD��EF ( )
���4=_____( )
�ߡ�1=��4
���1=_____( )
��DG��BC( )
���ADG=��C( )
 ������
������������������������Ҫ��Ϥƽ���ߵ����ʺ��ж�������ȷ���������������ɣ���Ҫע��ƽ���ߵ����ʺ��ж����ۺ����ã�
�����������BD��AC��EF��AC����֪����
���2=��3=90�㣬
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���4=��5����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�1=��4����֪����
���1=��5��������������
��DG��BC���ڴ�����...
������
������������������������Ҫ��Ϥƽ���ߵ����ʺ��ж�������ȷ���������������ɣ���Ҫע��ƽ���ߵ����ʺ��ж����ۺ����ã�
�����������BD��AC��EF��AC����֪����
���2=��3=90�㣬
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���4=��5����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�1=��4����֪����
���1=��5��������������
��DG��BC���ڴ�����... ��֪(x2��px��8)(x2��3x��q)��չ��ʽ�в���x2��x3���p��q��ֵ��
 p��3��q��1.
�����������������������ʽ�ij˷���������ɺ��ݲ������ϵ��Ϊ0��⼴��.
����������ߣ�x2+px+8����x2��3x+q��
=x4��3x3+qx2+px3��3px2+pqx+8x2��24x+8q
=x4+��p��3��x3+��q��3p+8��x2+��pq��24��x+8q��
�߳˻��в���x2��x3�
��p��3=0��q��3p+8=0��
��p=...
p��3��q��1.
�����������������������ʽ�ij˷���������ɺ��ݲ������ϵ��Ϊ0��⼴��.
����������ߣ�x2+px+8����x2��3x+q��
=x4��3x3+qx2+px3��3px2+pqx+8x2��24x+8q
=x4+��p��3��x3+��q��3p+8��x2+��pq��24��x+8q��
�߳˻��в���x2��x3�
��p��3=0��q��3p+8=0��
��p=... 
