如果将长度为a﹣2,a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是____________
 a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5.
a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5. 如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=__,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__.
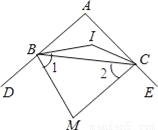
 140°; 40°.
【解析】∵∠A=100°,
∵∠ABC+∠ACB=180°?100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=∠ABC+∠ACB= (∠ABC+∠ACB)= ×80°=40°,
∴∠BIC=180°?(∠IBC+∠ICB)=180°?40°=140°,
∵∠...
140°; 40°.
【解析】∵∠A=100°,
∵∠ABC+∠ACB=180°?100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=∠ABC+∠ACB= (∠ABC+∠ACB)= ×80°=40°,
∴∠BIC=180°?(∠IBC+∠ICB)=180°?40°=140°,
∵∠... 如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是__.
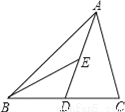
 6
【解析】试题分析:三角形的中线将三角形分成面积相等的两部分,则△ABD的面积=△ABC的面积=12,△ABE的面积=△ABD的面积=6.
6
【解析】试题分析:三角形的中线将三角形分成面积相等的两部分,则△ABD的面积=△ABC的面积=12,△ABE的面积=△ABD的面积=6. 一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
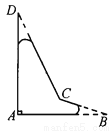
 不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格.
不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格. 如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
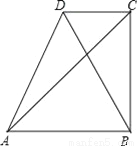
 6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm.
6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
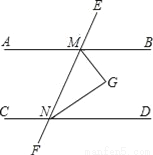
∴中AB边上的高等于6cm. 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=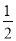 ∠BMN
∠BMN
同理∠GNM=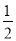 ∠DNM.
∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
 已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(...
已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(... 已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.
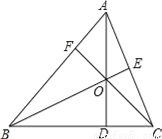
 120°.
【解析】试题分析:先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
试题解析:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠...
120°.
【解析】试题分析:先根据三角形的内角和定理求出∠ABE、∠ACF的度数,再根据三角形内角和定理求出∠EBO+∠FCB的度数,即可求出∠BOC.
试题解析:在△ABC中,∵∠BAC=60°,三条高AD、BE、CF相交于点O.
∴∠BEA=90°,∠CFA=90°,
∴∠ABE=30°,∠ACF=30°,
∴∠OBD+∠OCB=180°﹣∠BAC﹣∠OBD﹣∠... 如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
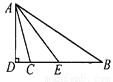
 35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,...
35°.
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
【解析】
在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,... 如图,在Rt△ABC中,∠C=90°,若sinA=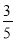 ,则cosB的是
,则cosB的是
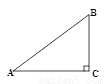
A. 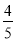 B.
B. 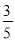 C.
C. 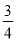 D.
D. 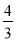
 B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B.
B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B. 在△ABC中,∠A=105°,∠B=45°,cosC的值是( )
A.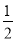 B.
B.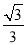 C.
C.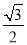 D.
D.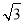
 C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C.
C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C.