题目内容
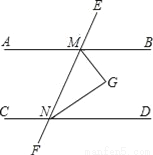
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=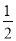 ∠BMN
∠BMN
同理∠GNM=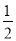 ∠DNM.
∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
 已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(...
已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(...
 科学实验活动册系列答案
科学实验活动册系列答案先化简,再求值: 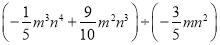 ,其中
,其中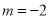 ,
, 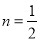 .
.
 【解析】试题分析:根据多项式除以单项式的法则进行化简,再把字母的值代入运算即可.
试题解析:原式,
当, 时,
原式.
【解析】试题分析:根据多项式除以单项式的法则进行化简,再把字母的值代入运算即可.
试题解析:原式,
当, 时,
原式. 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1, 在乙种地板上最终停留在黑色区域的概率为P2, 则( )
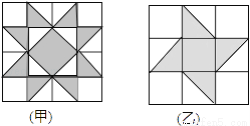
A. P1>P2 B. P1<P2 C. P1=P2 D. 以上都有可能
 A
【解析】试题分析:根据题意可知: ,则,故选A.
A
【解析】试题分析:根据题意可知: ,则,故选A. 如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan∠DBC 的值为 ( )
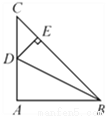
A. 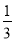 B.
B. 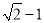 C.
C. 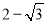 D.
D. 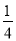
 A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A.
A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值
A. 也扩大3倍 B. 缩小为原来的
C. 都不变 D. 有的扩大,有的缩小
 C
【解析】试题分析:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选C.
C
【解析】试题分析:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选C. 如果将长度为a﹣2,a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是____________
 a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5.
a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5. 如图:(1)AD⊥BC,垂足为D,则AD是__的高,∠__=∠__=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫__,∠__=∠__=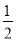 ∠__,AH叫__;
∠__,AH叫__;
(3)若AF=FC,则△ABC的中线是__;
(4)若BG=GH=HF,则AG是__的中线,AH是__的中线.
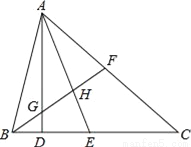
 BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线...
BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线... 如图所示,请你把下列梯形分成四个全等的四边形.
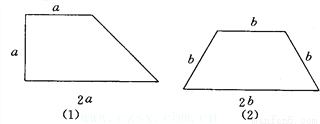
 见解析
【解析】试题分析:这两个梯形都是比较特殊的梯形,一个是直角梯形,一个是等腰梯形,因为要分为四个全等的四边形,因此分得的四个四边形与原梯形的形状是一样的,只是各相应的边长变为原来相应边长的一半,据此进行分割即可得.
试题解析:如图所示:
见解析
【解析】试题分析:这两个梯形都是比较特殊的梯形,一个是直角梯形,一个是等腰梯形,因为要分为四个全等的四边形,因此分得的四个四边形与原梯形的形状是一样的,只是各相应的边长变为原来相应边长的一半,据此进行分割即可得.
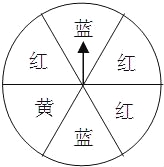
试题解析:如图所示: 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A.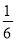 B.
B.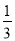 C.
C.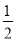 D.
D.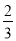
 A
【解析】
试题解析:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率=.
故选A.
A
【解析】
试题解析:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率=.
故选A. 
