题目内容
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
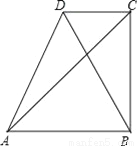
 6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm.
6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm.
练习册系列答案
相关题目
已知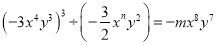 ,求
,求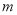 ,
, 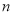 的值.
的值.
 ,
【解析】试题分析:根据单项式的除法法则即可求出, 的值.
试题解析:左边,
,
,
.
所以, ,
解得, .
,
【解析】试题分析:根据单项式的除法法则即可求出, 的值.
试题解析:左边,
,
,
.
所以, ,
解得, . 一个袋中装有2个红球,3个蓝球和5个白球,它们除颜色外完全相同,现在从中任意摸出一个球,则P(摸到红球)等于( )
A. 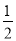 B.
B. 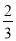 C.
C. 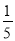 D.
D. 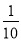
 C
【解析】袋中有2个红球,3个蓝球和5个白球,故共有球10个,所以从中任意摸出一个球,则P(摸到红球)=,故选C.
C
【解析】袋中有2个红球,3个蓝球和5个白球,故共有球10个,所以从中任意摸出一个球,则P(摸到红球)=,故选C. 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为( ).(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)
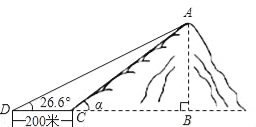
A.164m B.178m C.200m D.1618m
 C.
【解析】
试题分析:首先在Rt△ABC中,根据坡角的正切值用AB表示出BC,然后在Rt△DBA中,用BA表示出BD,根据BD与BC之间的关系列出方程求解即可.∵在Rt△ABC中,=tanα=1,∴BC=AB,∵在RtADB中,∴=tan26.6°=0.50,即:BD=2AB,∵BD﹣BC=CD=200,∴2AB﹣AB=200,解得:AB=200米.
故选:C.
C.
【解析】
试题分析:首先在Rt△ABC中,根据坡角的正切值用AB表示出BC,然后在Rt△DBA中,用BA表示出BD,根据BD与BC之间的关系列出方程求解即可.∵在Rt△ABC中,=tanα=1,∴BC=AB,∵在RtADB中,∴=tan26.6°=0.50,即:BD=2AB,∵BD﹣BC=CD=200,∴2AB﹣AB=200,解得:AB=200米.
故选:C. 在△ABC中,∠A=105°,∠B=45°,cosC的值是( )
A.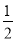 B.
B.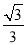 C.
C.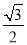 D.
D.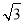
 C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C.
C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C. 如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=__度.
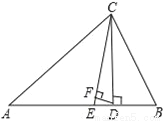
 74°
【解析】试题解析:
∵CE平分∠ACB,CD⊥AB于D,
∵DF⊥CE,
故答案为:74.
74°
【解析】试题解析:
∵CE平分∠ACB,CD⊥AB于D,
∵DF⊥CE,
故答案为:74. 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
 37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm.
37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm. 已知△ABC≌△A′B′C′,∠C=25°,BC=6 cm,AC=4 cm,你能得出△A′B′C′中哪些角的大小,哪些边的长度?
 ∠C’=25°,B’C’=6 cm,A’C’=4cm
【解析】试题分析:根据全等三角形的性质即可得.
试题解析:∵△ABC≌△A′B′C′,
∴∠C′=∠C=25°,
B′C′=BC=6cm,
A′C′=AC=4cm.
∠C’=25°,B’C’=6 cm,A’C’=4cm
【解析】试题分析:根据全等三角形的性质即可得.
试题解析:∵△ABC≌△A′B′C′,
∴∠C′=∠C=25°,
B′C′=BC=6cm,
A′C′=AC=4cm. 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )

A. B.
B. C.
C.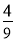 D.
D.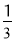
 C.
【解析】
试题分析:如图所示:所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个,
能构成轴对称图形的有所标数据1,2,3,4,共4个,则所得到的阴影图形恰好是轴对称图形的概率为:.
故选:C.
C.
【解析】
试题分析:如图所示:所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个,
能构成轴对称图形的有所标数据1,2,3,4,共4个,则所得到的阴影图形恰好是轴对称图形的概率为:.
故选:C. 
