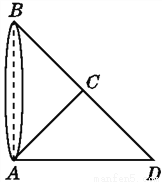
如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
证明见解析.
【解析】试题分析：根据SAS即可证明△ACB≌△ACD，由此即可解决问题．
试题解析：因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
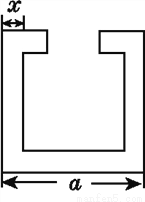
所以AB=AD. 如图,已知零件的外径为a,要求它的厚度x,动手制作一个简单的工具,利用三角形全等的知识,求出x.
.
【解析】试题分析：可设计如图所示的工具,利用△AOB≌△COD即可求解.
试题解析：可设计如图所示的工具,其中O为AC,BD的中点.
在△AOB和△COD中,
所以△AOB≌△COD(SAS).
所以AB=CD.所以测量出C,D之间的距离,CD的长就是A,B间的距离.
因为AB=a-2x,所以x==. 如图,在△ABC中,D为AB的中点,AD=5 cm,∠B=∠C,BC=8 cm.
(1)若点P在线段BC上以3 cm/s的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动.
①若点Q的速度与点P的速度相等,经过1 s后,请说明△BPD≌△CQP.
②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?
(2)若点P以3 cm/s的速度从点B向点C运动,同时点Q以5 cm/s的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?
（1）说明见解析；（2）当点Q的运动速度为cm/s时,能使△BPD≌△CPQ.（3）10s.
【解析】试题分析：（1）①根据等腰三角形的性质得到∠B=∠C，再加上BP=CQ=3，PC=BD=5，则可判断△BPD与△CQP全等；
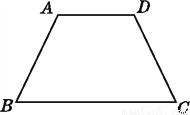
②设点Q的运动速度为xcm/s，则BP=3t，CQ=xt，CP=8-3t，当△BPD≌△CQP，则BP=CQ，CP=BD；然后分别建立关于t和v的方程，再解方程... 如图,AB=DC,∠A=∠D.试说明:∠ABC=∠DCB.
说明见解析.
【解析】试题分析：连接AC、BD，利用“边角边”证明△ABD和△DCA全等，根据全等三角形对应边相等可得AC=BD，再利用“边边边”证明△ABC和△DCB全等，根据全等三角形对应角相等证明即可．
试题解析：证明：如图，连接AC、BD，
在△ABD和△DCA中，
，
∴△ABD≌△DCA（SAS），
∴AC=BD，
在△ABC和△DCB中，
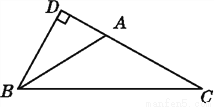
... 如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC交CA的延长线于点D,求∠ABD的度数.
30°.
【解析】试题分析：利用三角形的内角和为180°即可得到∠ABC或∠C的度数，进而利用外角可求得∠DAB的度数，从而求得∠ABD的度数．
试题解析：∵∠BAC=4∠ABC=4∠C，
∴∠BAC+∠ABC+∠C=180°，
即∠C=∠ABC=180×=30°，
∴∠DAB=∠C+∠ABC=30°+30°=60°，
∵BD⊥AC，
∴∠BDA=90°，... 农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20 m,求这块试验田的面积.
400m2.
【解析】试题分析：可延长DE至F，使EF=BC，可得△ABC≌△AEF，连AC，AD，AF，可将五边形ABCDE的面积转化为两个△ADF的面积，进而求出结论．
试题解析：如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
因为
所以△ABC≌△AEF(SAS).
所以AC=AF.
在△ACD与△AFD中,因为
所以△A... 到三角形三个顶点的距离都相等的点是这个三角形的（ ）
A. 三条高的交点 B. 三条角平分线的交点
C. 三条中线的交点 D. 三条边的垂直平分线的交点
D
【解析】【解析】
到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点，故选D． 如图，△ABC中，∠BAC=100°，DF，EG分别是AB，AC的垂直平分线，则∠DAE等于（ ）
A. 50° B. 45° C. 30° D. 20°
D
【解析】试题解析：根据线段的垂直平分线性质，可得AD=BD，AE=CE．
故∠EAC=∠ECA，∠ABD=∠BAD．
因为∠BAC=100°，∠ABD+∠ACE=180°-100°=80°，
∴∠DAE=100°-∠BAD-∠EAC=20°．
故选D. 如图，在△ABC中，DE是边AB的垂直平分线，BC=8cm，AC=5cm，则△ADC的周长为（ ）
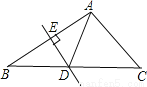
A. 14cm B. 13cm C. 11cm D. 9cm
B
【解析】试题解析：∵DE是边AB的垂直平分线
∴BD=AD
∴△ADC的周长为AC+DC+AD=AC+BC=5+8=13cm．
故选B. 已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是70cm和48cm，则△ABC的腰和底边长分别为（ ）
A．24cm和22cm B．26cm和18cm
C．22cm和26cm D．23cm和24cm
C
【解析】
试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出△DBC的周长=AC+BC，再根据两个三角形的周长求出AB，然后BC的值即可．
【解析】
∵AB的垂直平分线交AC于D，
∴AD=BD，
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC，
∵△ABC和△DBC的周长分别是70cm和48cm，
∴...