题目内容
如图,△ABC中,∠BAC=100°,DF,EG分别是AB,AC的垂直平分线,则∠DAE等于( )

A. 50° B. 45° C. 30° D. 20°
 D
【解析】试题解析:根据线段的垂直平分线性质,可得AD=BD,AE=CE.
故∠EAC=∠ECA,∠ABD=∠BAD.
因为∠BAC=100°,∠ABD+∠ACE=180°-100°=80°,
∴∠DAE=100°-∠BAD-∠EAC=20°.
故选D.
D
【解析】试题解析:根据线段的垂直平分线性质,可得AD=BD,AE=CE.
故∠EAC=∠ECA,∠ABD=∠BAD.
因为∠BAC=100°,∠ABD+∠ACE=180°-100°=80°,
∴∠DAE=100°-∠BAD-∠EAC=20°.
故选D.
在一些美术字中,有的汉字是轴对称图形,下面4个汉字中,可以看作是轴对称图形的是( )
吉 祥 如 意
(A)吉 (B)祥 (C)如 (D)意
 A.
【解析】
试题分析:根据轴对称图形的概念,在一个平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;四个选项中只有选项A符合要求,故答案选A.
A.
【解析】
试题分析:根据轴对称图形的概念,在一个平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;四个选项中只有选项A符合要求,故答案选A. 下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. 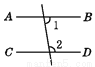 B.
B. 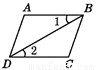 C.
C. 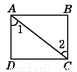 D.
D. 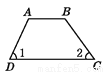
 B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B
B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B 下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. 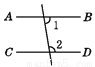 B.
B. 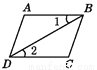 C.
C. 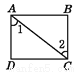 D.
D. 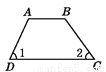
 B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B
B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B 如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数.
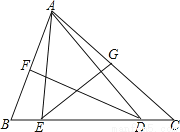
 36°
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质分别求出∠DAC和∠BAE的度数,计算得到∠EAD的度数.
试题解析:∵∠C=40°,∠B=68°,
∴∠BAC=72°,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=68°,
∴∠DAC=4°,...
36°
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到DA=DB,EA=EC,根据等腰三角形的性质分别求出∠DAC和∠BAE的度数,计算得到∠EAD的度数.
试题解析:∵∠C=40°,∠B=68°,
∴∠BAC=72°,
∵DF是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=68°,
∴∠DAC=4°,... 如图,在△ABC中,D为AB的中点,AD=5 cm,∠B=∠C,BC=8 cm.
(1)若点P在线段BC上以3 cm/s的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动.
①若点Q的速度与点P的速度相等,经过1 s后,请说明△BPD≌△CQP.
②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?
(2)若点P以3 cm/s的速度从点B向点C运动,同时点Q以5 cm/s的速度从点C向点A运动,它们都依次沿△ABC三边运动,则经过多长时间,点Q第一次在△ABC的哪条边上追上点P?

 (1)说明见解析;(2)当点Q的运动速度为cm/s时,能使△BPD≌△CPQ.(3)10s.
【解析】试题分析:(1)①根据等腰三角形的性质得到∠B=∠C,再加上BP=CQ=3,PC=BD=5,则可判断△BPD与△CQP全等;
②设点Q的运动速度为xcm/s,则BP=3t,CQ=xt,CP=8-3t,当△BPD≌△CQP,则BP=CQ,CP=BD;然后分别建立关于t和v的方程,再解方程...
(1)说明见解析;(2)当点Q的运动速度为cm/s时,能使△BPD≌△CPQ.(3)10s.
【解析】试题分析:(1)①根据等腰三角形的性质得到∠B=∠C,再加上BP=CQ=3,PC=BD=5,则可判断△BPD与△CQP全等;
②设点Q的运动速度为xcm/s,则BP=3t,CQ=xt,CP=8-3t,当△BPD≌△CQP,则BP=CQ,CP=BD;然后分别建立关于t和v的方程,再解方程... 某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CB的长度也为30 cm,依据是( )
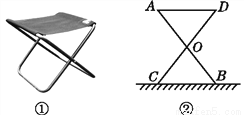
A. SAS B. ASA C. SSS D. AAS
 A
【解析】试题解析:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=30cm,
∴CB=30cm.
故选A.
A
【解析】试题解析:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=30cm,
∴CB=30cm.
故选A. 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
(1)求∠EBG的度数.
(2)求CE的长.
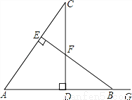
 (1)138°;(2)3.
【解析】试题分析:(1)根据全等求出∠EBA的度数,根据邻补角的定义求出即可;
(2)根据全等三角形的性质得出AC=AB=9,AE=AD=6,即可求出答案.
试题解析:(1)∵△ABE≌△ACD,
∴∠EBA=∠C=42°,
∴∠EBG=180°-42°=138°;
(2)∵△ABE≌△ACD,
∴AC=AB=9,AE=AD=6...
(1)138°;(2)3.
【解析】试题分析:(1)根据全等求出∠EBA的度数,根据邻补角的定义求出即可;
(2)根据全等三角形的性质得出AC=AB=9,AE=AD=6,即可求出答案.
试题解析:(1)∵△ABE≌△ACD,
∴∠EBA=∠C=42°,
∴∠EBG=180°-42°=138°;
(2)∵△ABE≌△ACD,
∴AC=AB=9,AE=AD=6... 当x=-2时,代数式ax3+bx+1的值是2 017,那么当x=2时,代数式ax3+bx+1的值是____.
 -2015
【解析】∵当x=-2时,代数式ax3+bx+1的值是2 017,
∴-8a-2b+1=2017,
即8a+2b=-2016.
∴当x=2时, ax3+bx+1=8a+2b+1=-2016+1=-2015.
-2015
【解析】∵当x=-2时,代数式ax3+bx+1的值是2 017,
∴-8a-2b+1=2017,
即8a+2b=-2016.
∴当x=2时, ax3+bx+1=8a+2b+1=-2016+1=-2015. 
