题目内容
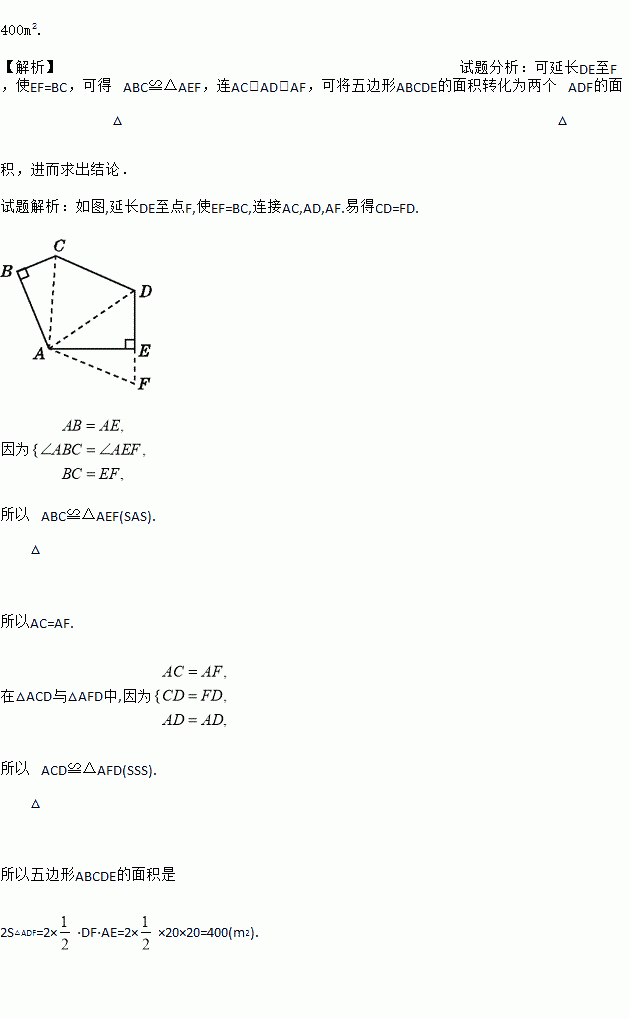
农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20 m,求这块试验田的面积.
400m2.
【解析】试题分析：可延长DE至F，使EF=BC，可得△ABC≌△AEF，连AC，AD，AF，可将五边形ABCDE的面积转化为两个△ADF的面积，进而求出结论．
试题解析：如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
因为
所以△ABC≌△AEF(SAS).
所以AC=AF.
在△ACD与△AFD中,因为
所以△A...
（12分）若a、b互为相反数，b、c互为负倒数，并且m的立方等于它本身．
（1）试求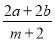
﹣ac值；
（2）若a＞1，且m=﹣1，S=|2a﹣3b|﹣2|b﹣m|﹣|b+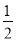
|，试求4（2a﹣S）+2（2a﹣S）﹣（2a﹣S）的值．
（3）若m＞0，且x为有理数时，|x+m|﹣|x﹣m|+1是否存在最大值，若存在，求出这个最大值，并求出x的取值范围；若不存在，请说明理由．
（1）-1；（2）；（3）当x时,取最大值为3
【解析】试题分析：（1）先根据a、b互为相反数，b、c互为倒数，得出a+b=0，bc=1，再代入所求代数式进行计算；
（2）根据a＞1及m的立方等于它本身把S进行化简，再代入所求代数式进行计算；
（3）根据若m>0，可知m=1，当m=1时，代入|x+m|-|x-m|+1，再根据绝对值的性质去掉绝对值符号，求出代数式的值；
【解... 如图,与∠B是同旁内角的角有( )
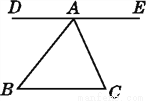
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】与∠B是同旁内角的角有∠C, ∠BAC, ∠BAE共3个.
故选C. 如图,与∠B是同旁内角的角有( )
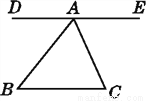
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】与∠B是同旁内角的角有∠C, ∠BAC, ∠BAE共3个.
故选C. 如图，已知线段AB的垂直平分线CP交AB于点P，且AP=2PC，现欲在线段AB上求作两点D，E，使其满足AD=DC=CE=EB，对于以下甲、乙两种作法：
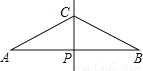
甲：分别作∠ACP、∠BCP的平分线，分别交AB于D、E，则D、E即为所求；乙：分别作AC、BC的垂直平分线，分别交AB于D、E，则D、E两点即为所求．下列说法正确的是（ ）
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确，乙错误 D. 甲错误，乙正确
D
【解析】试题解析：甲：虽然CP=AP，
但∠A≠∠ACP，
即∠A≠∠ACD．甲不正确；
乙∵CP是线段AB的中垂线，
∴△ABC是等腰三角形，即AC=BC，∠A=∠B，
作AC、BC之中垂线分别交AB于D、E，
∴∠A=∠ACD，∠B=∠BCE，
∵∠A=∠B，
∴∠A=∠ACD，∠B=∠BCE，
∵AC=BC，
∴△ACD≌... 如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
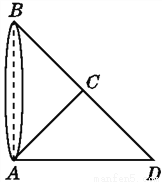
证明见解析.
【解析】试题分析：根据SAS即可证明△ACB≌△ACD，由此即可解决问题．
试题解析：因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD. 如图，将两根钢条AA′，BB′ 的中点O钉在一起，使AA′，BB′ 能绕点O自由转动，就做成一个测量工具，测A′B′ 的长即等于内槽宽AB，那么判定△OAB ≌△OA′B′的理由是（ ）．
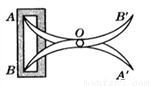
A. 边角边 B. 角边角 C. 边边边 D. 斜边直角边
A
【解析】由题意得边角边可得全等.故选A. 如图,已知△ABD≌△CDB,∠ABD=∠CDB,写出其余的对应边和对应角.
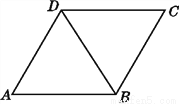
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析：∵△ABD≌△CDB，
∴∴AB的对应边是CD，AD的对应边是CB，BD的对应边是DB，
∠A的对应角是∠C，∠ADB的对应角是∠CBD，∠ACB的对应角是∠ECD. 若(2x＋1)0＝1，则x的取值范围是_____.
x≠-
【解析】任何一个不等于零的数的零次幂都等于1.由此可得2x+1≠0，解得，所以当(2x＋1)0＝1，x的取值范围是.