10.关于x的方程2x2+ax+b=0有两个不相等的实数根,且较小的根为2,则下列结论:
①2a+b<0;
②ab<0;
③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;
④抛物线y=2x2+ax+b-2的顶点在第四象限.
其中正确的结论有( )
①2a+b<0;
②ab<0;
③关于x的方程2x2+ax+b+2=0有两个不相等的实数根;
④抛物线y=2x2+ax+b-2的顶点在第四象限.
其中正确的结论有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
9.已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么当自变量x取m-1时,下列结论中正确的是( )
| A. | m-1的函数值小于0 | B. | m-1的函数值大于0 | ||
| C. | m-1的函数值等于0 | D. | m-1的函数值与0的大小关系不确定 |
7.下列函数中属于二次函数的是( )
| A. | y=2x-1 | B. | y=ax2-1 | C. | y=2(x-1)2-2x2 | D. | y=(x-1)($\sqrt{2}x+π$) |
6.在△ABC中,已知∠A,∠B都是锐角,且sinA=$\frac{1}{2}$,tanB=1,则∠C的度数为( )
| A. | 75° | B. | 105° | C. | 60° | D. | 45° |
5.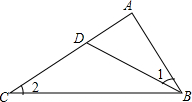 如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
 如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.已知α是锐角,cosα=$\frac{1}{3}$,则tanα的值是( )
| A. | $\frac{\sqrt{3}}{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
3.如图所示的三个矩形中,其中相似形是( )


| A. | 甲与乙 | B. | 乙与丙 | C. | 甲与丙 | D. | 以上都不对 |
2.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.
(1)如果小红家每月用水15吨,水费是30元,如果每月用水23吨,水费是47.8元
(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费如何用x代数式表示.
(3)如果小明家第二季度交纳水费的情况如下:
小明家这个季度共用水多少立方米?
0 311095 311103 311109 311113 311119 311121 311125 311131 311133 311139 311145 311149 311151 311155 311161 311163 311169 311173 311175 311179 311181 311185 311187 311189 311190 311191 311193 311194 311195 311197 311199 311203 311205 311209 311211 311215 311221 311223 311229 311233 311235 311239 311245 311251 311253 311259 311263 311265 311271 311275 311281 311289 366461
(1)如果小红家每月用水15吨,水费是30元,如果每月用水23吨,水费是47.8元
(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费如何用x代数式表示.
(3)如果小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 47.8元 |
