题目内容
4.已知α是锐角,cosα=$\frac{1}{3}$,则tanα的值是( )| A. | $\frac{\sqrt{3}}{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
分析 根据sin2α+cos2α=1,可得 sinα,根据正切函数与正弦函数、余弦函数的定义,可得答案.
解答 解:由sin2α+cos2α=1,α是锐角,cosα=$\frac{1}{3}$,得
sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{2\sqrt{2}}{3}$,
tanα=$\frac{sinα}{cosα}$=$\frac{\frac{2\sqrt{2}}{3}}{\frac{1}{3}}$=2$\sqrt{2}$,
故选:B.
点评 本题考查了同角三角函数关系,利用sin2α+cos2α=1,tanα=$\frac{sinα}{cosα}$是解题关键.

练习册系列答案
相关题目
19.下列几种说法正确的是( )
| A. | -a一定是负数 | B. | |a|一定是正数 | ||
| C. | 平方后等于9的数是3 | D. | 0的相反数是0 |
9.已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么当自变量x取m-1时,下列结论中正确的是( )
| A. | m-1的函数值小于0 | B. | m-1的函数值大于0 | ||
| C. | m-1的函数值等于0 | D. | m-1的函数值与0的大小关系不确定 |
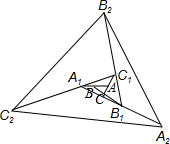 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为142015.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为142015.