题目内容
6．在△ABC中，已知∠A，∠B都是锐角，且sinA=$\frac{1}{2}$，tanB=1，则∠C的度数为（ ）| A． | 75° | B． | 105° | C． | 60° | D． | 45° |
分析 根据特殊角三角函数值，可得A、B的值，根据三角形的内角和，可得答案．
解答 解：由∠A，∠B都是锐角，且sinA=$\frac{1}{2}$，tanB=1，得
A=30°，B=45°．
由三角形的内角和，得
C=180°-∠A-∠B=180°-30°-45°=105°，
故选：B．
点评 本题考查了三角形的内角和定理，利用特殊角三角函数值得出∠A、∠B的值是解题关键．
练习册系列答案
相关题目
18．下列命题是真命题的是（ ）
| A． | 有一个角为60°的三角形是等边三角形 | |
| B． | 底边相等的两个等腰三角形全等 | |
| C． | 有一个角是40°，腰相等的两个等腰三角形全等 | |
| D． | 一边上的中线等于这条边的一半的三角形是直角三角形 |
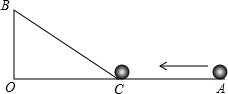如图，∠AOB=90°，OA=36cm，OB=12cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？