11.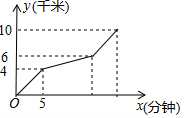 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )| A. | 15分钟 | B. | 20分钟 | C. | 25分钟 | D. | 30分钟 |
10. 如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
 如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )| A. | 甲校的女生比乙校的女生多 | B. | 甲校的女生比乙校的女生少 | ||
| C. | 甲校与乙校的女生一样多 | D. | 甲校与乙校男生共是2250人 |
9.下列四个图案中,具有一个共有的性质,

那么下面四个数中,满足上述共有性质的一个是( )

那么下面四个数中,满足上述共有性质的一个是( )
| A. | 228 | B. | 707 | C. | 808 | D. | 609 |
6.某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值.
0 298370 298378 298384 298388 298394 298396 298400 298406 298408 298414 298420 298424 298426 298430 298436 298438 298444 298448 298450 298454 298456 298460 298462 298464 298465 298466 298468 298469 298470 298472 298474 298478 298480 298484 298486 298490 298496 298498 298504 298508 298510 298514 298520 298526 298528 298534 298538 298540 298546 298550 298556 298564 366461
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值.
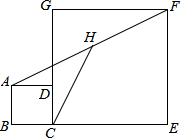 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.