题目内容
8.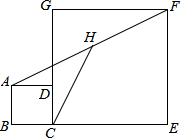 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.
分析 过H作HM⊥BE于M,求出CM,根据梯形的中位线求出HM,根据勾股定理求出即可.
解答 解:过H作HM⊥BE于M,则∠HMC=90°,
∵正方形ABCD和正方形CEFG,
∴AB=BC=1,EF=CE=4,∠B=∠E=90°,
∴HM∥AB∥FE,
∵H为AF大的中点,
∴M为BE的中点,
∴HM=$\frac{1}{2}$(AB+EF)=$\frac{1}{2}×$(1+4)=$\frac{5}{2}$,
∵BC=1,CE=2,
∴BM=2.5,
∴CM=1.5,
在Rt△HMC中,由勾股定理得:CH=$\sqrt{H{M}^{2}+C{M}^{2}}$=$\frac{1}{2}\sqrt{34}$,
故答案为:$\frac{1}{2}\sqrt{34}$.
点评 本题考查了正方形性质,勾股定理,梯形的性质等知识点,能构造直角三角形是解此题的关键.

练习册系列答案
相关题目
 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)
如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)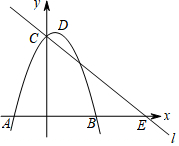 如图,抛物线y=-x2+x+6与x轴交于A,B两点,点A在点B的左侧,抛物线与y轴交于C,抛物线的顶点为D,直线l过点C交x轴于E(6,0).
如图,抛物线y=-x2+x+6与x轴交于A,B两点,点A在点B的左侧,抛物线与y轴交于C,抛物线的顶点为D,直线l过点C交x轴于E(6,0).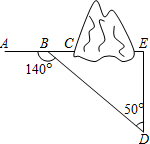 如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°,求开挖点E到点D的距离.(结果精确到1米)
如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°,求开挖点E到点D的距离.(结果精确到1米)