题目内容
15.(1)化简:$\frac{a-2}{a+3}$÷$\frac{{a}^{2}-4}{{a}^{2}+6a+9}$(2)解方程组:$\left\{\begin{array}{l}{x-2y=-5}\\{2x+y=0}\end{array}\right.$.
分析 (1)根据分式的运算即可求出答案.
(2)根据方程组的解法即可求出答案.
解答 解:(1)原式=$\frac{a-2}{a+3}$×$\frac{(a+3)^{2}}{(a+2)(a-2)}$
=$\frac{a+3}{a+2}$
(2)由2x+y=0可知:y=-2x,
将y=-2x代入x-2y=-5
∴x+4x=-5
x=-1
将x=-1代入y=-2x
y=2
∴方程组的解为:$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
10. 如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
 如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )| A. | 甲校的女生比乙校的女生多 | B. | 甲校的女生比乙校的女生少 | ||
| C. | 甲校与乙校的女生一样多 | D. | 甲校与乙校男生共是2250人 |
4.若反比例函数y=-$\frac{4}{x}$的图象经过第二象限的点(a,-a),则a的值为( )
| A. | 2或-2 | B. | -2 | C. | 2 | D. | 4 |
17.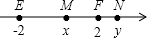 如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
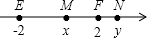 如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
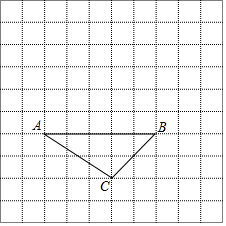 如图,已知△ABC.
如图,已知△ABC.