8.小明根据华师版八年级下册教材P37学习内容,对函数y=$\frac{1}{2}$x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
其中n=-3;
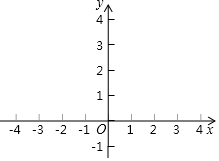
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为0.
(4)进一步探究函数的图象发现:
①若点A(xa,ya),点B(xb,yb)在函数y=$\frac{1}{2}{x}^{2}$的图象上;
当xa<xb<0时,ya与yb的大小关系是ya>yb;
当0<xa<xb时,ya与yb的大小关系是ya<yb;
②直线y1恰好经过函数的图象上的点(-2,2)与(1,0.5);当y<y1时,x的取值范围是-2<x<1.
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
| x | … | -4 | n | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | … |
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为0.
(4)进一步探究函数的图象发现:
①若点A(xa,ya),点B(xb,yb)在函数y=$\frac{1}{2}{x}^{2}$的图象上;
当xa<xb<0时,ya与yb的大小关系是ya>yb;
当0<xa<xb时,ya与yb的大小关系是ya<yb;
②直线y1恰好经过函数的图象上的点(-2,2)与(1,0.5);当y<y1时,x的取值范围是-2<x<1.

5.小张文具店每月一次性购进100件文具进行销售(能全部售出),有A,B两种文具可供选择,已知A型文具的进价是每件10元,B型文具的进价是每件15元,小张发现,所获总利润y(元)与A型文具的进货量x(件)之间存在着如下表所示的一次函数关系:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)在小张文具店中,B型文具的售价是23元;
(3)若在六月份,小张只有1300元,在进货量(100件)不变的前提下,六月份的最大利润是多少?
0 298047 298055 298061 298065 298071 298073 298077 298083 298085 298091 298097 298101 298103 298107 298113 298115 298121 298125 298127 298131 298133 298137 298139 298141 298142 298143 298145 298146 298147 298149 298151 298155 298157 298161 298163 298167 298173 298175 298181 298185 298187 298191 298197 298203 298205 298211 298215 298217 298223 298227 298233 298241 366461
| 购进A型文具x件 | … | 10 | 20 | 30 | 40 | 50 | … |
| 总利润y元 | … | 740 | 680 | 620 | 560 | 500 | … |
(2)在小张文具店中,B型文具的售价是23元;
(3)若在六月份,小张只有1300元,在进货量(100件)不变的前提下,六月份的最大利润是多少?
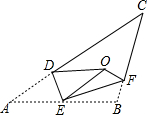 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为46°.
如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为46°.
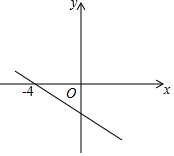 y=-2x-m的图象如图,关于x的不等式-2x-m>0的解集是x<-4.
y=-2x-m的图象如图,关于x的不等式-2x-m>0的解集是x<-4. 如图,在△ABC中,AD⊥BC于点D,BD=4厘米,DC=6厘米,AD=8厘米,动点P从点B出发,沿折线BA-AD运动,到D点停止,过点P作BC的平行线交折线DA-AB于点F,点E为AC的中点,动点Q沿A-E-A运动,过Q作BC的平行线交AD于点G,点P在BA上的速度为2$\sqrt{5}$厘米/秒,在AD上的速度为4厘米/秒,点Q的速度为$\frac{5}{2}$厘米/秒,点P、Q同时出发,有一点到达终点时另一点也停止运动,以P、F、Q、G为顶点的四边形的面积为y(厘米2),运动的时间为t(秒).
如图,在△ABC中,AD⊥BC于点D,BD=4厘米,DC=6厘米,AD=8厘米,动点P从点B出发,沿折线BA-AD运动,到D点停止,过点P作BC的平行线交折线DA-AB于点F,点E为AC的中点,动点Q沿A-E-A运动,过Q作BC的平行线交AD于点G,点P在BA上的速度为2$\sqrt{5}$厘米/秒,在AD上的速度为4厘米/秒,点Q的速度为$\frac{5}{2}$厘米/秒,点P、Q同时出发,有一点到达终点时另一点也停止运动,以P、F、Q、G为顶点的四边形的面积为y(厘米2),运动的时间为t(秒).