题目内容
7．【知识拓展】（1）你能对a3+b3因式分解吗？
（2）求最大正整数n，使得n3+2017，能被n+13整除．
分析 （1）根据公式法对其进行分解因式即可；
（2）根据题意列出算式，变形后得到180能整除n+13，即可确定出最大的正整数n的值．
解答 解：（1）能，a3+b3=（a+b）（a2-ab+b2）；
（2）要使（n3+2017）÷（n+13）=$\frac{{n}^{3}+2017}{n+13}$=$\frac{（n+13）（{n}^{2}-13n+169）-180}{n+13}$=n2-13n+169-$\frac{180}{n+13}$为整数，
必须180能整除n+13，
则n的最大值为167．
点评 此题考查了整式的除法，熟练掌握单项式除单项式法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．
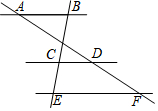如图，已知AB∥CD∥EF，AD：AF=3：5，BE=15，那么CE的长等于（ ）
如图，已知AB∥CD∥EF，AD：AF=3：5，BE=15，那么CE的长等于（ ）| A． | 9 | B． | 6 | C． | $\frac{15}{2}$ | D． | $\frac{9}{2}$ |
如图，在矩形OABC中，OA=8，OC=4，OA、OC分别在x轴与y轴上，D为OA上一点，且CD=AD．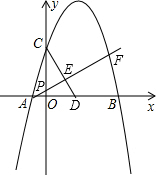
如图，已知抛物线y=ax2+bx+3与x轴交于A，B两点（点A在原点左侧，点B在原点右侧），与y轴交于点C，且OB=OC=3OA，点P为线段OC上一动点，射线AP与抛物线交于点F，CD⊥AF于点E，交x轴于点D．
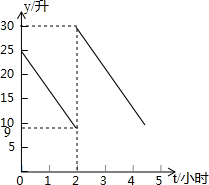张师傅驾车从甲地到乙地，两地相距S千米，汽车出发前油箱有油25升，途中加油若干升，加油前、后汽车都以同样的速度匀速行驶，已知油箱中剩余油量y（升）与行驶时间t（小时）之间的关系如图所示．张师傅途中加油21升．