11.阅读下面材料,并解答其后的问题:
定义:两组领边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.
类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
(1)表格中①、②分别填写的内容是:
①轴对称图形;
②一条对角线垂直平分另一条对角线.
(2)演绎论证:证明筝形有关对角线的性质.
已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证:AC垂直平分BD.
证明:
(3)运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积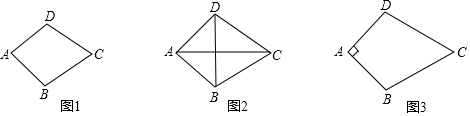
定义:两组领边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.
类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
| 四边形 | 示例图形 | 对称性 | 边 | 角 | 对角线 |
| 平行 四边形 |  | 两组对边分别平行,两组对边分别相等 | 两组对边分别平行,两组对边分别相等. | 两组对角 分别相等. | 对角线互相平分. |
| 等腰 梯形 |  | ①轴对称图形 | 两组邻边分别相等 | 有一组对角相等 | ②一条对角线垂直平分另一条对角线 |
①轴对称图形;
②一条对角线垂直平分另一条对角线.
(2)演绎论证:证明筝形有关对角线的性质.
已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证:AC垂直平分BD.
证明:
(3)运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积

4.已知a+b=2,a-b=-3,则a2-b2的值为( )
0 297403 297411 297417 297421 297427 297429 297433 297439 297441 297447 297453 297457 297459 297463 297469 297471 297477 297481 297483 297487 297489 297493 297495 297497 297498 297499 297501 297502 297503 297505 297507 297511 297513 297517 297519 297523 297529 297531 297537 297541 297543 297547 297553 297559 297561 297567 297571 297573 297579 297583 297589 297597 366461
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | -5 |
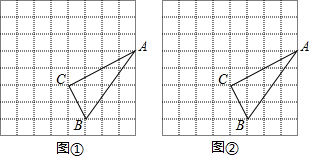 如图,小方格的边长为1,△ABC为格点三角形.
如图,小方格的边长为1,△ABC为格点三角形.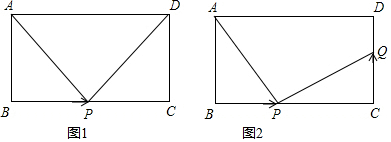
 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题: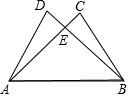 如图所示,AD=BC,AC=BD,试说明:DE=CE.
如图所示,AD=BC,AC=BD,试说明:DE=CE.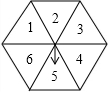 如图所示的是一个正六边形转盘被分成6个全等的等边三角形,指针位置固定,转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数 (指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.
如图所示的是一个正六边形转盘被分成6个全等的等边三角形,指针位置固定,转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数 (指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.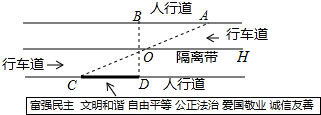 杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:
杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下: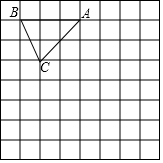 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.