题目内容
7.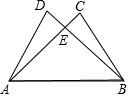 如图所示,AD=BC,AC=BD,试说明:DE=CE.
如图所示,AD=BC,AC=BD,试说明:DE=CE.
分析 可先证△ABD≌△BAC,可求得∠D=∠C,则可证明△ADE≌△BCE,可证得结论.
解答 解:
在△ADB和△BCA中
$\left\{\begin{array}{l}{AD=BC}\\{BD=AC}\\{AB=BA}\end{array}\right.$
∴△ADB≌△BCA(SSS),
∴∠D=∠C,
在△ADE和△BCE中
$\left\{\begin{array}{l}{∠D=∠C}\\{∠DEA=∠CEB}\\{AD=BC}\end{array}\right.$
∴△ADE≌△BCE(AAS),
∴DE=CE.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、全等三角形的对应角相等)是解题的关键.

练习册系列答案
相关题目

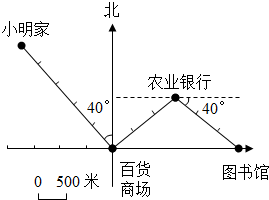 小明家在百货商场的北偏西40°方向2500米处,图书馆在农业银行东偏南40°方向1500米处,如图是小明坐出租车从家去图书馆的路线图,已知出租车在3千米以内(含3千米)按起步价9元计算,以后每增加1千米车费就增加2元.请你按图中提供的信息算一算,小明一共要花多少元出租车费?
小明家在百货商场的北偏西40°方向2500米处,图书馆在农业银行东偏南40°方向1500米处,如图是小明坐出租车从家去图书馆的路线图,已知出租车在3千米以内(含3千米)按起步价9元计算,以后每增加1千米车费就增加2元.请你按图中提供的信息算一算,小明一共要花多少元出租车费?
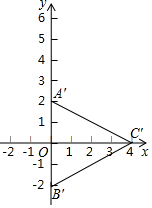
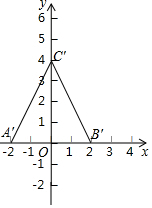
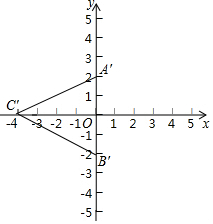
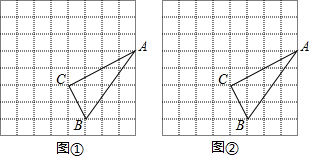 如图,小方格的边长为1,△ABC为格点三角形.
如图,小方格的边长为1,△ABC为格点三角形.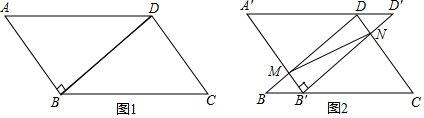
 如图,把△ABC绕点A顺时针旋转20°至△ADE,且点B的对应点D在BC边上,则∠ADE的度数为80°.
如图,把△ABC绕点A顺时针旋转20°至△ADE,且点B的对应点D在BC边上,则∠ADE的度数为80°.