题目内容
5.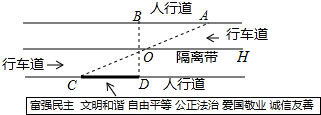 杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:
杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好阅读完对面人行道宣传墙上的社会主义核心价值观标语CD,创设数学情境如下:如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于点O,OD⊥CD,垂足为D,已知AB=20米,根据上述信息杨阳同学求出了标语CD的长度.(请将杨阳同学的解答过程补充完整)
解:因为AB∥DC,
所以∠ABO=∠CDO(依据是两直线平行,内错角相等)
又因为DO⊥CD,
所以∠CDO=90°,
所以∠ABO=90°,
所以BO⊥AB.
因为相邻两平行线间的距离相等,
所以BO=DO.
在△BOA和△DOC中,
∠ABO=∠CDO,
BO=DO,
∠AOB=∠COD,(依据是对顶角相等)
所以△BOA≌△DOC(ASA).
所以CD=AB=20米.
分析 由AB∥CD,利用平行线的性质可得∠ABO=∠CDO,由垂直的定义可得∠CDO=90°,易得OB⊥AB,由相邻两平行线间的距离相等可得OD=OB,利用ASA定理可得△ABO≌△CDO,由全等三角形的性质可得结果.
解答 解:因为AB∥DC,
所以∠ABO=∠CDO(依据是两直线平行,内错角相等)
又因为DO⊥CD,
所以∠CDO=90°,
所以∠ABO=90°,
所以BO⊥AB.
因为相邻两平行线间的距离相等,
所以 BO=DO,
在△BOA和△DOC中,
∠ABO=∠CDO,
BO=DO,
∠AOB=∠COD,(依据是对顶角相等)
所以△BOA≌△DOC(ASA).
所以CD=AB=20米.
故答案为:两直线平行,内错角相等;ABO;BO;DO;BO;DO;对顶角相等;ASA.
点评 本题主要考查了平行线的性质和全等三角形的判定及性质定理,关键是掌握全等三角形的判定方法.

练习册系列答案
相关题目
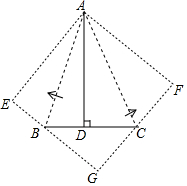 如图,△ABC中,∠BAC=45°,AD⊥BC于D,BD=3,AD=8,求DC的长.
如图,△ABC中,∠BAC=45°,AD⊥BC于D,BD=3,AD=8,求DC的长.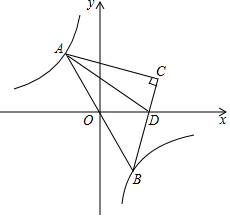 如图,等腰直角三角形ABC的直角顶点C在第一象限,顶点A、B分别在函数y=$\frac{8}{x}$图象的两个分支上,且AB经过原点O,BC与x轴相交于点D,连接AD,已知AD平分四边形AODC的面积.
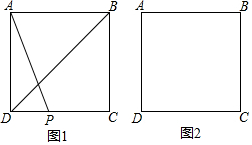
如图,等腰直角三角形ABC的直角顶点C在第一象限,顶点A、B分别在函数y=$\frac{8}{x}$图象的两个分支上,且AB经过原点O,BC与x轴相交于点D,连接AD,已知AD平分四边形AODC的面积.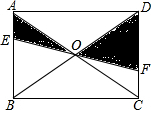 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形的面积为s,那么阴影部分的面积是$\frac{S}{4}$.
如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形的面积为s,那么阴影部分的面积是$\frac{S}{4}$.