6.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | -(-1)2015与(-1)2016 | D. | -(-3)与+(-3) |
3.如图是若干个边长均为1cm的正方形组成的网格,正方形的顶点也叫格点,如果一个多边形的顶点全是格点,这个多边形叫格点多边形,这样的多边形的面积计算起来很方便,只要数一下多边形各边上格点数的总和及这个多边形内的格点数就可以用公式计算,现在我们就来探究这个公式.
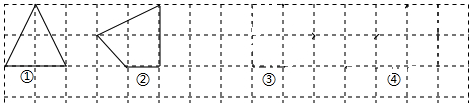
探究一 格点多边形内只有一个格点. 请根据图形填写下列表格
探究二 格点多边形内只有两个格点
请在网格中画出符合条件的两个格点多边形,根据你画出的图形,完善表格中相应的内容.
探究三 当格点多边形内只有三个格点并且各边上格点数的总和为n个时,格点多边形的面积S=$\frac{1}{2}$n+2(用含n的代数式表示)
猜想 当格点多边形内有m个格点并且各边上格点总数的和为n个时,格点多边形的面积S=$\frac{1}{2}$n+m-1(用含m,n的代数式表示)

探究一 格点多边形内只有一个格点. 请根据图形填写下列表格
探究二 格点多边形内只有两个格点
请在网格中画出符合条件的两个格点多边形,根据你画出的图形,完善表格中相应的内容.
| 图形编号 | 多边形内格点数/个 | 多边形各边上格点数的总和/个 | 多边形的面积/cm2 |
| ① | 1 | 4 | 2 |
| ② | 1 | 5 | $\frac{5}{2}$ |
| ③ | 2 | 10 | 6 |
| ④ | 2 | 4 | 3 |
猜想 当格点多边形内有m个格点并且各边上格点总数的和为n个时,格点多边形的面积S=$\frac{1}{2}$n+m-1(用含m,n的代数式表示)
2. 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )| A. | 6$\sqrt{3}$+12 | B. | 6$\sqrt{3}$+16 | C. | 18 | D. | 6 |
1.ABCD是四边形,AB=2,BC=4,CD=7,则线段AD的取值范围是( )
| A. | 0<AD<7 | B. | 2<AD<7 | C. | 0<AD<13 | D. | 1<AD<13 |
18.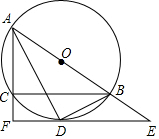 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
0 297328 297336 297342 297346 297352 297354 297358 297364 297366 297372 297378 297382 297384 297388 297394 297396 297402 297406 297408 297412 297414 297418 297420 297422 297423 297424 297426 297427 297428 297430 297432 297436 297438 297442 297444 297448 297454 297456 297462 297466 297468 297472 297478 297484 297486 297492 297496 297498 297504 297508 297514 297522 366461
 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
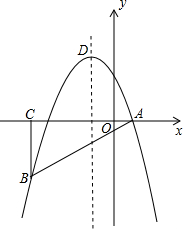 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.
如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.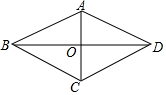 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.