题目内容
1．ABCD是四边形，AB=2，BC=4，CD=7，则线段AD的取值范围是（ ）| A． | 0＜AD＜7 | B． | 2＜AD＜7 | C． | 0＜AD＜13 | D． | 1＜AD＜13 |
分析 在△ABC中，根据第三边的范围应大于已知两边的差，小于两边的和，得2＜AC＜6．在△ACD中，根据三角形的三边关系进行求解．
解答 
解：连接AC，
∵AB=2，BC=4，
在△ABC中，根据三角形的三边关系，4-2＜AC＜2+4，即2＜AC＜6．
在△ACD中，根据三角形的三边关系，得7-6＜AD＜7+6，即1＜AD＜13．
故AD的取值范围是1＜AD＜13．
故选：D．
点评 本题综合考查了三角形的三边关系．连接AC，求出AC的取值范围是解题关键．
练习册系列答案
相关题目
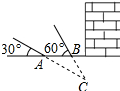如图，某武警部队在一次地震抢险救灾行动中，探险队员在相距4米的水平地面A，B两处均探测出建筑物下方C处有生命迹象，已知在A处测得探测线与地面的夹角为30°，在B处测得探测线与地面的夹角为60°，求该生命迹象C处与地面的距离．（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
6．下列各组数据中，结果相等的是（ ）
| A． | （-1）4与-14 | B． | -|-3|与-（-3） | C． | -（-1）2015与（-1）2016 | D． | -（-3）与+（-3） |
13．下列说法中，不正确的是（ ）
| A． | 3是（-3）2的算术平方根 | B． | -2与$\sqrt{{{（{-2}）}^2}}$互为相反数 | ||
| C． | $\sqrt{24}=±2\sqrt{6}$ | D． | $\sqrt{81}$平方根是±3 |
如图，直线AB、CD相交于O，∠AOC=28°，OE平分∠AOD，求∠EOC的度数．