题目内容
2. 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )| A. | 6$\sqrt{3}$+12 | B. | 6$\sqrt{3}$+16 | C. | 18 | D. | 6 |
分析 如图,连接PA延长PA交⊙A于E,连接PB,延长PB交⊙B于F.观察图象可知,要使得PE+PF的值最大,当点P与点C重合时,PE+PF的值最大.
解答 解:如图,连接PA延长PA交⊙A于E,连接PB,延长PB交⊙B于F.
观察图象可知,要使得PE+PF的值最大,当点P与点C重合时,PE+PF的值最大,
易知AC=2×6×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
∴PE=6$\sqrt{3}$+4+8=6$\sqrt{3}$+12.
故选A.
点评 本题考查菱形的性质、等边三角形的性质,点与圆的位置关系等知识,解题的关键是理解题意,正确寻找使得PE+PF的值最大时的位置,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列方程①x-2=$\frac{1}{x}$;②x=0;③2x-y=3;④x2-3x=0;⑤x2-2x=3-3x+x2;⑥$\frac{x}{3}$=2x-1,其中是一元一次方程的是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
14.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(-a,b)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
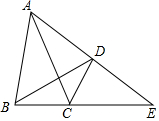 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.