20. 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
(1)试说明a=2时,四边形OMAB是菱形.
(2)当a的值分别取1,2,3时,分别计算s的值,将其填入如表
(3)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,当四边形OMAB为正方形时,a=2,m=$\frac{1}{2}$.
(4)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,s=4m3(用含m的代数式表示)
 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.(1)试说明a=2时,四边形OMAB是菱形.
(2)当a的值分别取1,2,3时,分别计算s的值,将其填入如表
| a | 1 | 2 | 3 |
| s |
(4)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,s=4m3(用含m的代数式表示)
19.一公司打算招聘一名口语能力较强的英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,它们的各项成绩(百分制)如下表所示听、说、读、写成绩按照7:8:3:2的比确定,计算两名应试着的平均成绩(百分制).从他们的成绩看,应该录取谁?
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 83 | 80 | 83 | 75 |
14. 已知直线a∥b∥c,则下列结论:①$\frac{BC}{AC}$=$\frac{ED}{DF}$;②$\frac{BC}{DE}$=$\frac{AB}{EF}$;③$\frac{BC}{AB}$=$\frac{BE}{AF}$,其中正确的有( )
已知直线a∥b∥c,则下列结论:①$\frac{BC}{AC}$=$\frac{ED}{DF}$;②$\frac{BC}{DE}$=$\frac{AB}{EF}$;③$\frac{BC}{AB}$=$\frac{BE}{AF}$,其中正确的有( )
0 285669 285677 285683 285687 285693 285695 285699 285705 285707 285713 285719 285723 285725 285729 285735 285737 285743 285747 285749 285753 285755 285759 285761 285763 285764 285765 285767 285768 285769 285771 285773 285777 285779 285783 285785 285789 285795 285797 285803 285807 285809 285813 285819 285825 285827 285833 285837 285839 285845 285849 285855 285863 366461
 已知直线a∥b∥c,则下列结论:①$\frac{BC}{AC}$=$\frac{ED}{DF}$;②$\frac{BC}{DE}$=$\frac{AB}{EF}$;③$\frac{BC}{AB}$=$\frac{BE}{AF}$,其中正确的有( )
已知直线a∥b∥c,则下列结论:①$\frac{BC}{AC}$=$\frac{ED}{DF}$;②$\frac{BC}{DE}$=$\frac{AB}{EF}$;③$\frac{BC}{AB}$=$\frac{BE}{AF}$,其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,四边形ABCD中,AB≠CD,E、F、G、H分别是AB、BD、CD、AC的中点.
如图,四边形ABCD中,AB≠CD,E、F、G、H分别是AB、BD、CD、AC的中点. 如图,A(4,0),B(0,4),直线y=$\frac{1}{3}$x与直线AB交于点C.
如图,A(4,0),B(0,4),直线y=$\frac{1}{3}$x与直线AB交于点C. 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.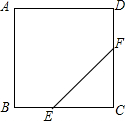 如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.
如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.