题目内容
16. 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.
分析 联立直线和双曲线解析式可求得A、B坐标,再求得C点坐标,再利用待定系数法可分别求得直线AC和直线BC的解析式,可求得P点坐标及直线BC与y轴的交点坐标,再利用三角形的面积可求得答案.
解答 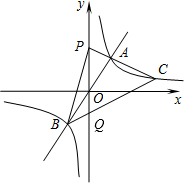 解:如图,设直线BC交y轴于点Q,
解:如图,设直线BC交y轴于点Q,
联立直线和双曲线解析式可得$\left\{\begin{array}{l}{y=\frac{3}{2}x}\\{y=\frac{6}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$,
∴A(2,3),B(-2,-3),
由C点横坐标为6,代入双曲线解析式可得y=$\frac{6}{6}$=1,
∴C(6,1),
设直线AC解析式为y=kx+b,把A、C坐标代入可得$\left\{\begin{array}{l}{2k+b=3}\\{6k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直线AC解析式为y=-$\frac{1}{2}$x+4,
∴P(0,4),
设直线BC解析式为y=mx+n,把B、C坐标代入可得$\left\{\begin{array}{l}{-2m+n=-3}\\{6m+n=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=-2}\end{array}\right.$,
∴直线BC解析式为y=$\frac{1}{2}$x-2,
∴Q(0,-2),
∴PQ=4-(-2)=6,
∴S△PBC=S△PQB+S△PQC=$\frac{1}{2}$×6×[6-(-2)]=24,
故答案为:24.
点评 本题主要考查直线与双曲线的交点问题,求得直线BC、直线AC与y轴的交点坐标是解题的关键.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | 45×104 | B. | 4.5×105 | C. | 0.45×106 | D. | 4.5×106 |
| A. | 存在负整数 | B. | 存在正整数 | C. | 存在负分数 | D. | 不存在正分数 |
| A. | 3-a>3-b | B. | a-3>b-3 | C. | -$\frac{a}{3}$<-$\frac{b}{3}$ | D. | a2<b2 |
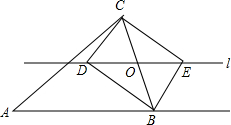 如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E,
如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E, 如图,A(4,0),B(0,4),直线y=$\frac{1}{3}$x与直线AB交于点C.
如图,A(4,0),B(0,4),直线y=$\frac{1}{3}$x与直线AB交于点C.