12. 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )
 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )| A. | 22.5° | B. | 36° | C. | 45° | D. | 90° |
8.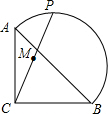 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )| A. | $\sqrt{2}$π | B. | π | C. | 2$\sqrt{2}$ | D. | 2 |
7. 如图,将△ABC绕点A逆时针旋转得到△AB′C′,若B′落到BC边上,∠B=50°,则∠CB′C′的度数为( )
如图,将△ABC绕点A逆时针旋转得到△AB′C′,若B′落到BC边上,∠B=50°,则∠CB′C′的度数为( )
 如图,将△ABC绕点A逆时针旋转得到△AB′C′,若B′落到BC边上,∠B=50°,则∠CB′C′的度数为( )
如图,将△ABC绕点A逆时针旋转得到△AB′C′,若B′落到BC边上,∠B=50°,则∠CB′C′的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
5.我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
| 图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
| 平移 |  | (1)AB=A′B′,AB∥A′B′ | AA′=BB′ AA′∥BB′ |
| 轴对称 | 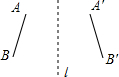 | (2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上. | (3)l垂直平分AA′ |
| 旋转 |  | AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. | (4)OA=OA′,∠AOA′=∠BOB′ |
4.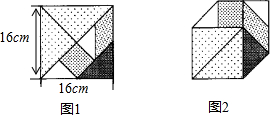 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
3.$\sqrt{9}$=( )
0 284210 284218 284224 284228 284234 284236 284240 284246 284248 284254 284260 284264 284266 284270 284276 284278 284284 284288 284290 284294 284296 284300 284302 284304 284305 284306 284308 284309 284310 284312 284314 284318 284320 284324 284326 284330 284336 284338 284344 284348 284350 284354 284360 284366 284368 284374 284378 284380 284386 284390 284396 284404 366461
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 已知一次函数y=2x+4
已知一次函数y=2x+4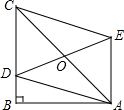 如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是4.
如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是4.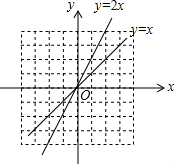 如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数y=2x的图象.
如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变,得到函数y=2x的图象.