题目内容
7．
如图，将△ABC绕点A逆时针旋转得到△AB′C′，若B′落到BC边上，∠B=50°，则∠CB′C′的度数为（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
分析 依据旋转的性质可求得AB=AB′，∠AB′C′的度数，依据等边对等角的性质可得到∠B=∠BB′A，于是可得到∠CB′C′的度数．
解答 解：由旋转的性质可知：AB=AB′，∠B=∠AB′C′=50°．
∵AB=AB′，
∴∠B=∠BB′A=50°．
∴∠BB′C′=50°+50°=100°．
∴∠CB′C′=180°-100°=80°．
故选：D．
点评 本题主要考查的是旋转的性质、等腰三角形的性质，求得∠AB′C′和∠BB′A的度数是解题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2$\sqrt{3}$），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线第一次垂直时，点P的坐标为（1，$\sqrt{3}$）．
2．方程x2+x-12=0的两个根为（ ）
| A． | x1=-2，x2=6 | B． | x1=-6，x2=2 | C． | x1=-3，x2=4 | D． | x1=-4，x2=3 |
12．
如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（ ）
如图，直线a∥b，△ABC为等腰直角三角形，∠BAC=90°，则∠1的度数是（ ）| A． | 22.5° | B． | 36° | C． | 45° | D． | 90° |
19．与$\sqrt{2}$是同类二次根式的为（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{3}$ | C． | $\sqrt{12}$ | D． | $\sqrt{6}$ |
17．
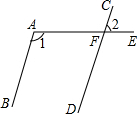如图，AB∥CD，射线AE交CD于点F，若∠1=115°，则∠2的度数是（ ）
如图，AB∥CD，射线AE交CD于点F，若∠1=115°，则∠2的度数是（ ）| A． | 55° | B． | 65° | C． | 75° | D． | 85° |