题目内容
9.将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象.若该图象在直线y=2下方的点的横坐标x满足0<x<3,则b的取值范围为-4≤b≤-2.分析 先解不等式2x+b<2时,得x<$\frac{2-b}{2}$;再求出函数y=2x+b沿x轴翻折后的解析式为y=-2x-b,解不等式-2x-b<2,得x>-$\frac{2+b}{2}$;根据x满足0<x<3,得出-$\frac{2+b}{2}$=0,$\frac{2-b}{2}$=3,进而求出b的取值范围.
解答 解:∵y=2x+b,
∴当y<2时,2x+b<2,解得x<$\frac{2-b}{2}$;
∵函数y=2x+b沿x轴翻折后的解析式为-y=2x+b,即y=-2x-b,
∴当y<2时,-2x-b<2,解得x>-$\frac{2+b}{2}$;
∴-$\frac{2+b}{2}$<x<$\frac{2-b}{2}$,
∵x满足0<x<3,
∴-$\frac{2+b}{2}$=0,$\frac{2-b}{2}$=3,
∴b=-2,b=-4,
∴b的取值范围为-4≤b≤-2.
故答案为:-4≤b≤-2.
点评 本题考查了一次函数图象与几何变换,求出函数y=2x+b沿x轴翻折后的解析式是解题的关键.

练习册系列答案
相关题目
19.已知关于x的不等式ax-3x+2>5的一个解是-2,则a的取值范围为( )
| A. | a<$\frac{3}{2}$ | B. | a>$\frac{3}{2}$ | C. | a>-$\frac{9}{2}$ | D. | a<-$\frac{9}{2}$ |
4.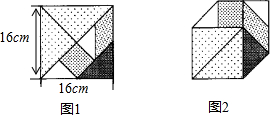 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
14. 如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
 如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
如图,在周长为20cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
1. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下结论错误的是( )| A. | ∠ABC=90° | B. | △OAD是等边三角形 | ||
| C. | OA=OB;OC=OB | D. | AC=BD |
 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.