题目内容
4.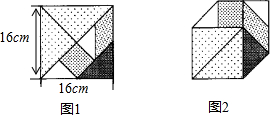 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
分析 由正方形的性质和勾股定理求出各板块的边长,即可求出凸六边形的周长.
解答 解: 如图所示:图形1:边长分别是:16,8$\sqrt{2}$,8$\sqrt{2}$;
如图所示:图形1:边长分别是:16,8$\sqrt{2}$,8$\sqrt{2}$;
图形2:边长分别是:16,8$\sqrt{2}$,8$\sqrt{2}$;
图形3:边长分别是:8,4$\sqrt{2}$,4$\sqrt{2}$;
图形4:边长是:4$\sqrt{2}$;
图形5:边长分别是:8,4$\sqrt{2}$,4$\sqrt{2}$;
图形6:边长分别是:4$\sqrt{2}$,8;
图形7:边长分别是:8,8,8$\sqrt{2}$;
∴凸六边形的周长=8+2×8$\sqrt{2}$+8+4$\sqrt{2}$×4=32$\sqrt{2}$+16(cm);
故答案为:32$\sqrt{2}$+16.
点评 本题考查了正方形的性质、勾股定理、等腰直角三角形的性质;熟练掌握正方形的性质,求出各板块的边长是解决问题的关键.

练习册系列答案
相关题目
14.一组数据:-3,1,4,1,-3,则这组数据的中位数是( )
| A. | -3 | B. | 1 | C. | 3 | D. | 4 |
15.如果(4a2-3ab2)÷M=-4a+3b2,那么单项式M等于( )
| A. | ab | B. | -ab | C. | -a | D. | -b |
14. 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )| A. | 100° | B. | 72° | C. | 64° | D. | 36° |
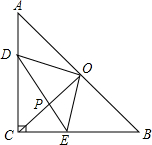 如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论: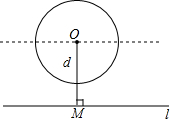 如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知: 如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.
如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB=22.5°.