20.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3,随机摸出一个小球,然后放回,再随机摸出一个小球,两次摸出的小球标号的和为5的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19.据大连市公安局统计,2016年全市约有410000人换二代居民身份证,将410000用科学记数法表示应为( )
| A. | 0.41×104 | B. | 41×104 | C. | 4.1×106 | D. | 4.1×105 |
17.将抛物线y=2x2+4x-5的图象向左平移2个单位,再向上平移1个单位,所得抛物线解析式是( )
| A. | y=2(x+1)2-7 | B. | y=2(x+1)2-6 | C. | y=2(x+3)2-6 | D. | y=2(x-1)2-6 |
15.某射击队要从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
小明根据统计结果计算了甲的平均数和方差,方法如下:
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
$\overline{{x}_{甲}}$=$\frac{1}{6}$(10+8+9+8+10+9)=9(环)
s2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$
请根据以上信息,解答下列问题:
(1)请参考小明的方法分别计算乙的平均数和方差;
(2)请根据调查结果,从平均数和方差的角度分析选谁去参加比赛较为合适?
14. 已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )
已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )
 已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )
已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )| A. |  | B. |  | C. |  | D. | 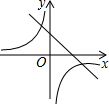 |
13.在一个不透明的袋子中有1个红球和1个白球,这些球除颜色外都相同,现从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,则两次摸到不同颜色的球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
12.下列四个数中,相反数是-$\frac{1}{5}$的数是( )
0 283258 283266 283272 283276 283282 283284 283288 283294 283296 283302 283308 283312 283314 283318 283324 283326 283332 283336 283338 283342 283344 283348 283350 283352 283353 283354 283356 283357 283358 283360 283362 283366 283368 283372 283374 283378 283384 283386 283392 283396 283398 283402 283408 283414 283416 283422 283426 283428 283434 283438 283444 283452 366461
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | -$\frac{1}{5}$ |
 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.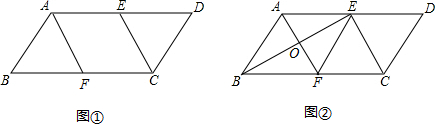
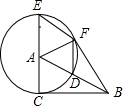 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.