题目内容
1. 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.
分析 根据锐角三角函数关系得出AD的长,再利用菱形的性质和勾股定理得出DE的长,进而求出答案.
解答 解:∵DE⊥AB,cosA=$\frac{3}{5}$,AE=3,
∴$\frac{AE}{AD}$=$\frac{3}{AD}$=$\frac{3}{5}$,
解得:AD=5,
则DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=4,
∵四边形ABCD是菱形,
∴AD=AB=5,
∴BE=2,
∴tan∠DBE=$\frac{DE}{EB}$=$\frac{4}{2}$=2.
故答案为:2.
点评 此题主要考查了菱形的性质以及锐角三角函数关系,正确得出EC的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )
如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )
 如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )
如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
11.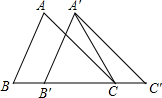 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
 如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30$\sqrt{6}$海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30$\sqrt{6}$海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)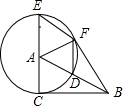 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF. 如图,点A是双曲线y=$\frac{8}{x}$(x>0)上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y=$\frac{2}{x}$(x>0)于点B、C,连接BC,设点A的横坐标为a.
如图,点A是双曲线y=$\frac{8}{x}$(x>0)上的动点,过A作AB∥x轴,AC∥y轴,分别交双曲线y=$\frac{2}{x}$(x>0)于点B、C,连接BC,设点A的横坐标为a.