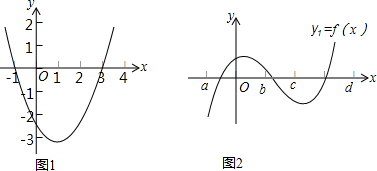
0 282976 282984 282990 282994 283000 283002 283006 283012 283014 283020 283026 283030 283032 283036 283042 283044 283050 283054 283056 283060 283062 283066 283068 283070 283071 283072 283074 283075 283076 283078 283080 283084 283086 283090 283092 283096 283102 283104 283110 283114 283116 283120 283126 283132 283134 283140 283144 283146 283152 283156 283162 283170 366461
 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
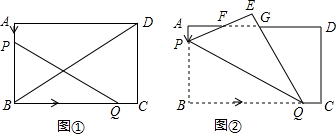 如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).
如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).
 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α. 已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.
已知,如图,抛物线y=-x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα-tanβ=2,OC2=OA•OB.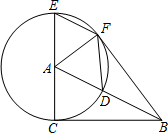 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF. 如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).
如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).