题目内容
10.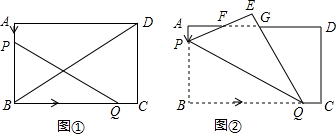 如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).
如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).(1)当t=$\frac{60}{23}$s时,△BPQ为等腰三角形;
(2)当BD平分PQ时,求t的值;
(3)如图②,将△BPQ沿PQ折叠,点B的对应点为E,PE、QE分别与AD交于点F、G.
探索:是否存在实数t,使得AF=EF?如果存在,求出t的值:如果不存在,说明理由.
分析 (1)由运动得出BP=BQ,求出t,即可;
(2)由PM∥AD,得出$\frac{PM}{AD}=\frac{BP}{AB}$,表示出PM,从而求出t,即可;
(3)先判断出△AEP≌△FEG,表示出BH,HQ,CQ,再由勾股定理计算即可.
解答 解:(1)当BP=BQ时,60-3t=20t,
∴t=$\frac{60}{23}$,
(2)如图1,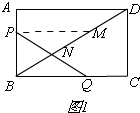
过P作PM∥AD,
∴$\frac{PM}{AD}=\frac{BP}{AB}$,
∴$\frac{PM}{90}=\frac{60-3t}{60}$,
∴PM=90-$\frac{9}{2}$t,
∵PN=NQ,PM=BQ,
∴90-$\frac{9}{2}$t=20t,
∴t=$\frac{180}{49}$,
(3)如图2,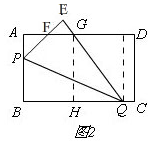
作GH⊥BQ,
∴PB=PF=60-3t,
∵AE=EF,∠AEP=∠FEG,∠A=∠F,
∴△AEP≌△FEG,
∴PE=EG,FG=AP,
∴AG=PF=60-3t=BH,
∴HQ=BQ-BH=20t-(60-3t)=23t-60,
GQ=FQ-FG=BQ-AP=17t,
根据勾股定理得,602=(17t)2-(23t-60)2
∴t1=4,t2=7.5(舍),
∴t=4
∴存在t=4,使AE=EF.
点评 此题是四边形综合题,主要考查了平行线分线段成比例定理,全等三角形的性质和判定,勾股定理,用时间t表示线段是解本题的关键.

练习册系列答案
相关题目
20.若2x3-ax2-5x+5=(2x2+ax-1)(x-b)+3,其中a,b为整数,则a+b的值为( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
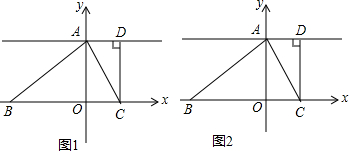
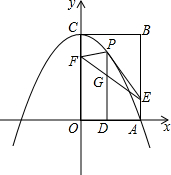 如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PD⊥OA于点D,点E(8,2),F(0,6),连接PE、PF、EF.
如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PD⊥OA于点D,点E(8,2),F(0,6),连接PE、PF、EF.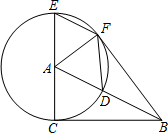 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.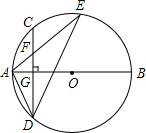 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论: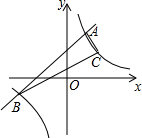 已知一次函数y1=x+5的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点,已知点A的横坐标为1.
已知一次函数y1=x+5的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点,已知点A的横坐标为1.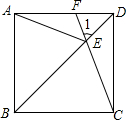 如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.
如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.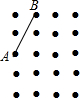 如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A、B,请在此点阵图中找一个阵点C,使得以点A、B、C为顶点的三角形是等腰三角形,则符合条件的点C有5个.
如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A、B,请在此点阵图中找一个阵点C,使得以点A、B、C为顶点的三角形是等腰三角形,则符合条件的点C有5个.