题目内容
8.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A和点B,如果△AMB为等腰直角三角形,我们把抛物线上A、B两点之间部分与线段AB围成的图形称为该抛物线的准蝶形,顶点M称为碟顶,线段AB的长称为碟宽.(1)抛物线y=$\frac{1}{2}$x2的碟宽为4,抛物线y=ax2(a>0)的碟宽为$\frac{2}{a}$.
(2)如果抛物线y=a(x-1)2-6a(a>0)的碟宽为6,那么a=$\frac{1}{3}$.
(3)将抛物线yn=anx2+bnx+cn(an>0)的准蝶形记为Fn(n=1,2,3,…),我们定义F1,F2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.如果Fn与Fn-1的相似比为$\frac{1}{2}$,且Fn的碟顶是Fn-1的碟宽的中点,现在将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②请判断F1,F2,…,Fn的碟宽的右端点是否在一条直线上?如果是,直接写出该直线的表达式;如果不是,说明理由.
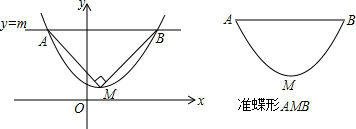
分析 (1)根据定义可算出y=ax2(a>0)的碟宽为$\frac{2}{a}$、碟高为$\frac{1}{a}$,由于抛物y=ax2+bx+c(a>0)可通过平移y=ax2(a>0)得到,得到碟宽为$\frac{2}{a}$、碟高为$\frac{1}{a}$,由此可得碟宽、碟高只与a有关,与别的无关,从而可得.
(2)由(1)的结论,根据碟宽易得a的值.
(3)①根据y1,容易得到y2.
②结合画图,易知h1,h2,h3,…,hn-1,hn都在直线x=2上,可以考虑hn∥hn-1,且都过Fn-1的碟宽中点,进而可得.画图时易知碟宽有规律递减,由此可得右端点的特点.对于“F1,F2,…,Fn的碟宽右端点是否在一条直线上?”,我们可以推测任意相邻的三点是否在一条直线上,如果相邻的三个点不共线则结论不成立,反之则成立,所以可以考虑基础的几个图形关系,利用特殊点求直线方程即可.
解答 解:(1)∵a>0,
∴y=ax2的图象大致如下: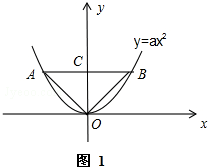
其必过原点O,记AB为其碟宽,AB与y轴的交点为C,连接OA,OB.
∵△DAB为等腰直角三角形,AB∥x轴,
∴OC⊥AB,
∴∠OCA=∠OCB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°,
∴△ACO与△BCO亦为等腰直角三角形,$\frac{1}{a}$∴AC=OC=BC,
∴xA=-yA,xB=yB,代入y=ax2,
∴A(-$\frac{1}{a}$,$\frac{1}{a}$),B($\frac{1}{a}$,),C(0,$\frac{1}{a}$),
∴AB=$\frac{2}{2}$,OC=$\frac{1}{a}$,
即y=ax2的碟宽为$\frac{2}{a}$.
抛物线y=$\frac{1}{2}$x2对应的a=$\frac{1}{2}$,得碟宽$\frac{2}{a}$为4;
故答案为4,$\frac{2}{a}$,
(2)抛物线y=a(x-1)2-6a(a>0)的碟宽为6,可看成y=ax2向右平移2个单位长度,再向下平移6a个单位长度后得到的图形,
∵平移不改变形状、大小、方向,
∴抛物线y=a(x-1)2-6a(a>0)的碟宽为6,的准碟形与抛物线y=ax2的准碟形全等,
∵抛物线y=ax2(a>0),碟宽为$\frac{2}{a}$,
∴$\frac{2}{a}$=6,
∴a=$\frac{1}{3}$,
故答案为$\frac{1}{3}$,
(3)①∵F1的碟宽:F2的碟宽=2:1,
∴$\frac{2}{{a}_{1}}=\frac{2}{{a}_{2}}$,
∵a1=$\frac{1}{3}$,
∴a2=$\frac{2}{3}$.
∵y=$\frac{1}{3}$(x-2)2-3的碟宽AB在x轴上(A在B左边),
∴A(-1,0),B(5,0),
∴F2的碟顶坐标为(2,0),
∴y2=$\frac{2}{3}$(x-2)2.
②∵Fn的准碟形为等腰直角三角形,
∴Fn的碟宽为2hn,
∵2hn:2hn-1=1:2,
∴hn=$\frac{1}{2}$hn-1=($\frac{1}{2}$)2hn-2=($\frac{1}{2}$)3hn-3=…=($\frac{1}{2}$)n+1h1,
∵h1=3,
∴hn=$\frac{3}{{2}^{n+1}}$.
∵hn∥hn-1,且都过Fn-1的碟宽中点,
∴h1,h2,h3,…,hn-1,hn都在一条直线上,
∵h1在直线x=2上,
∴h1,h2,h3,…,hn-1,hn都在直线x=2上,
∴Fn的碟宽右端点横坐标为2+$\frac{3}{{2}^{n+1}}$.
另,F1,F2,…,Fn的碟宽右端点在一条直线上,直线为y=-x+5.
分析如下:
考虑Fn-2,Fn-1,Fn情形,关系如图2,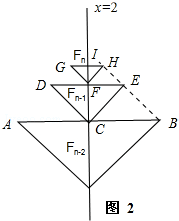
Fn-2,Fn-1,Fn的碟宽分别为AB,DE,GH;C,F,I分别为其碟宽的中点,都在直线x=2上,连接右端点,BE,EH.
∵AB∥x轴,DE∥x轴,GH∥x轴,
∴AB∥DE∥GH,
∴GH平行且等于FE,DE平行且等于CB,
∴四边形GFEH,四边形DCBE都为平行四边形,
∴HE∥GF,EB∥DC,
∵∠GFI=$\frac{1}{2}$∠GFH=$\frac{1}{2}$∠DCE=∠DCF,
∴GF∥DC,
∴HE∥EB,
∵HE,EB都过E点,
∴HE,EB在一条直线上,
∴Fn-2,Fn-1,Fn的碟宽的右端点是在一条直线,
∴F1,F2,…,Fn的碟宽的右端点是在一条直线.
∵F1:y1=$\frac{1}{3}$(x-2)2-3准碟形右端点坐标为(5,0),
F2:y2=$\frac{2}{3}$(x-2)2准碟形右端点坐标为(2+$\frac{3}{2}$,$\frac{3}{2}$),
∴待定系数可得过两点的直线为y=-x+5,
∴F1,F2,…,Fn的碟宽的右端点是在直线y=-x+5上.
点评 此题是二次函数综合题,主要考查了等腰直角三角形的性质,理解准碟形中的有关概念,和性质,相似准蝶形的性质,解本题的关键是准碟形中的性质的理解

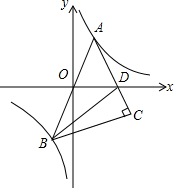 如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
 一辆动车从重庆开往成都,一辆高铁从成都开往重庆,两车同时出发,设动车离重庆的距离为y1(cm),高铁离重庆的距离为y2(km),动车行驶时间为t(h),变量y1,y2与t之间的关系图象如图所示:
一辆动车从重庆开往成都,一辆高铁从成都开往重庆,两车同时出发,设动车离重庆的距离为y1(cm),高铁离重庆的距离为y2(km),动车行驶时间为t(h),变量y1,y2与t之间的关系图象如图所示: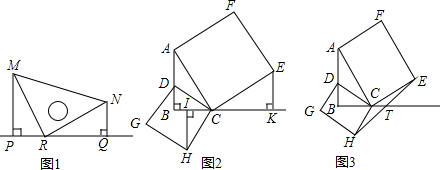
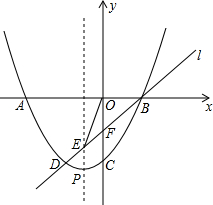 如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.
如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.