19.如果6m=a,那么我们称m为a的郎格数,记为m=f(a).有上述定义可知:6m=a和m=f(a)中的变量a与m所表示的关系为同一关系,并且有性质:若a、b均为正数,则f(ab)=f(a)+f(b),f($\frac{a}{b}$)=f(a)-f(b).
(1)根据郎格数的定义可得:
f(6)=1;f($\frac{1}{6}$)=-1;f($\frac{1}{36}$)=-2;
(2)根据郎格数的性质可得:
$①\frac{f({a}^{a})}{f(a)}$=a(a为正数)
②若f(2)=x(x≠0),则f(3)=1-x,f(4)=2x.
(3)若下表中与数a对应的郎格数f(a)有且只有一个是不正确的,请找出错误的郎格数,说明理由并改正.
(1)根据郎格数的定义可得:
f(6)=1;f($\frac{1}{6}$)=-1;f($\frac{1}{36}$)=-2;
(2)根据郎格数的性质可得:
$①\frac{f({a}^{a})}{f(a)}$=a(a为正数)
②若f(2)=x(x≠0),则f(3)=1-x,f(4)=2x.
(3)若下表中与数a对应的郎格数f(a)有且只有一个是不正确的,请找出错误的郎格数,说明理由并改正.
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f(a) | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
18. 如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
 如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
15.下列命题中,属于假命题的是( )
| A. | 如果a>b,那么-a<-b | |
| B. | 等角的余角相等 | |
| C. | 等式的两边同加上或同减去一个式子,结果仍为等式 | |
| D. | 如果a+b>0,那么a>0,b>0 |
14.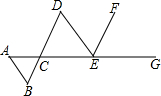 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )| A. | 0个 | B. | 1个 | C. | 3个 | D. | 5个 |
13.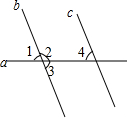 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )| A. | ∠2=115° | B. | ∠3=65° | C. | ∠4=65° | D. | ∠4=115° |
12.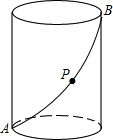 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )| A. | 2$\sqrt{{π}^{2}+4}$cm | B. | 4$\sqrt{{π}^{2}+4}cm$ | C. | 8$\sqrt{{π}^{2}+4}cm$ | D. | 无法确定 |
11. 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )
 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )| A. | 小于1m | B. | 等于1m | C. | 大于1m | D. | 以上都不对 |
10.一直角三角形的斜边长为15cm,其中一直角边长为5cm,则这个三角形的面积为( )
0 281734 281742 281748 281752 281758 281760 281764 281770 281772 281778 281784 281788 281790 281794 281800 281802 281808 281812 281814 281818 281820 281824 281826 281828 281829 281830 281832 281833 281834 281836 281838 281842 281844 281848 281850 281854 281860 281862 281868 281872 281874 281878 281884 281890 281892 281898 281902 281904 281910 281914 281920 281928 366461
| A. | 25$\sqrt{2}$cm2 | B. | 50$\sqrt{2}$cm2 | C. | $\frac{75}{2}c{m}^{2}$ | D. | 75cm2 |
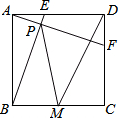 如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.
如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.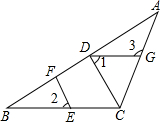 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.