题目内容
13．
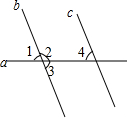如图，已知直线b，c被直线a所截，∠1=65°，若要判断b∥c，则下列所给条件正确的是（ ）| A． | ∠2=115° | B． | ∠3=65° | C． | ∠4=65° | D． | ∠4=115° |
分析 根据平行线的判定定理进行选择即可．
解答 解：∵∠1=65°，
∴∠3=65°，∠2=115°，
要使b∥c，
∠1=∠4或∠3=∠4，
故选C．
点评 本题考查了平行线的判定．正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
练习册系列答案
阅读快车系列答案
相关题目
3．
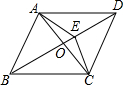如图，在菱形ABCD中，∠ABC=70°，AC与BD相交于点O，E是OD上一点，若有AE=DE，则下列说法不正确的是（ ）
如图，在菱形ABCD中，∠ABC=70°，AC与BD相交于点O，E是OD上一点，若有AE=DE，则下列说法不正确的是（ ）| A． | 点E是△ACD的内心 | B． | ∠DBC=35° | C． | CE=DE | D． | △ABO≌△CBO |
18．
如图，在△ABC中，∠ACB=90°，D为AB的中点，E为AC上一点，连接DE，并过点D作FD⊥ED，垂足为D，交BC于点F．若AC=BC=14，AE：EC=4：3，则tan∠EFC的值为（ ）
如图，在△ABC中，∠ACB=90°，D为AB的中点，E为AC上一点，连接DE，并过点D作FD⊥ED，垂足为D，交BC于点F．若AC=BC=14，AE：EC=4：3，则tan∠EFC的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则平行四边形ABCD的周长为18．
3．以下列各组数作为三角形的三边长，其中不能构成直角三角形的是（ ）
| A． | 1，1，$\sqrt{2}$ | B． | 12，16，20 | C． | 1，$\frac{4}{3}$，$\frac{5}{3}$ | D． | 1，2，2 |