题目内容
17.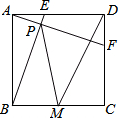 如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.
如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.
分析 首先作出点D关于BC的对称点D′从而可知当点P、M、D′在一条直线上时,路径最短,当点E与点D重合,点F与点C重合时,PG和GD′均最短,即PD′最短,然后由正方形的性质和轴对称图形的性质可知:PG=2,GD′=6,最后由勾股定理即可求得PD′的长,从而可求得MD+MP的最小值.
解答 解:如图作点D关于BC的对称点D′,连接PD′,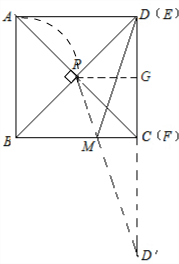
由轴对称的性质可知:MD=D′M,CD=CD′=4,
∴PM+DM=PM+MD′=PD′
过点P作PE垂直DC,垂足为G,
易证AF⊥BE,故可知P的轨迹为以AB为直径的四分之一圆弧上,当点E与点D重合,点F与点C重合时,PG和GD′均最短,
∴此时,PD′最短.
∵四边形ABCD为正方形,
∴PG=$\frac{1}{2}$AD=2,GC=$\frac{1}{2}$DC=2.
∴GD′=6.
在Rt△PGD′中,由勾股定理得:PD′=$\sqrt{P{G}^{2}+GD{'}^{2}}=\sqrt{{2}^{2}+{6}^{2}}=2\sqrt{10}$.
故答案为2$\sqrt{10}$
点评 本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.

练习册系列答案
相关题目
8.下列说法错误的是( )
| A. | 绝对值最小的数是0 | B. | 最小的自然数是1 | ||
| C. | 最大的负整数是-1 | D. | 绝对值小于2的整数是:1,0,-1 |
12.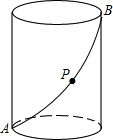 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )| A. | 2$\sqrt{{π}^{2}+4}$cm | B. | 4$\sqrt{{π}^{2}+4}cm$ | C. | 8$\sqrt{{π}^{2}+4}cm$ | D. | 无法确定 |
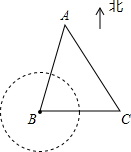 南沙群岛自古以来就是中国的领土,但南沙群岛中只哟部分岛屿受中国的控制,赤瓜礁就是其中之一.以赤瓜礁为圆心,在周围12海里范围内均属于禁区,不允许他国船只进入.今有一中国海监船(记作A)正以14海里/小时的速度在位于赤瓜礁(记作B)北偏东15°的海域中巡逻,海监船上的值班人员发现在赤瓜礁的正东方向24海里有一艘外国渔船(记作C),其正以10海里/小时的速度沿正西方向驶向赤瓜礁,中方立即向外国渔船发出警告,此时外国渔船在中国海监船的南偏东30°的方向上,如图所示.
南沙群岛自古以来就是中国的领土,但南沙群岛中只哟部分岛屿受中国的控制,赤瓜礁就是其中之一.以赤瓜礁为圆心,在周围12海里范围内均属于禁区,不允许他国船只进入.今有一中国海监船(记作A)正以14海里/小时的速度在位于赤瓜礁(记作B)北偏东15°的海域中巡逻,海监船上的值班人员发现在赤瓜礁的正东方向24海里有一艘外国渔船(记作C),其正以10海里/小时的速度沿正西方向驶向赤瓜礁,中方立即向外国渔船发出警告,此时外国渔船在中国海监船的南偏东30°的方向上,如图所示. 如图,能表示点到直线的距离的线段共有5条.
如图,能表示点到直线的距离的线段共有5条.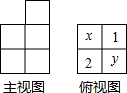 由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x=1或2,y=3.
由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,求x=1或2,y=3.