题目内容
10．一直角三角形的斜边长为15cm，其中一直角边长为5cm，则这个三角形的面积为（ ）| A． | 25$\sqrt{2}$cm2 | B． | 50$\sqrt{2}$cm2 | C． | $\frac{75}{2}c{m}^{2}$ | D． | 75cm2 |
分析 根据勾股定理求出另一条直角边，再根据三角形面积公式列式计算可得．
解答 解：根据勾股定理可知直角三角形的另一条直角边为：$\sqrt{1{5}^{2}-{5}^{2}}$=10$\sqrt{2}$cm，
则直角三角形面积为：$\frac{1}{2}×5×10\sqrt{2}$=25$\sqrt{2}$cm2，
故选：A．
点评 本题主要考查二次根式的实际应用，由勾股定理求直角边是解题前提、关键，根据三角形面积公式列出算式计算是基础．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
20．对于任意两个实数对（a，b），和（c，d），当且仅当a=c且b=d时，（a，b）=（c，d）．我们现在定义新运算“※”：（a，b）※（c，d）=（a2-c，b+d2）．若（2，x）※（y，5）=（3，34），则xy的值为（ ）
| A． | 3 | B． | -3 | C． | 9 | D． | -9 |
如图，能表示点到直线的距离的线段共有5条．
15．下列命题中，属于假命题的是（ ）
| A． | 如果a＞b，那么-a＜-b | |
| B． | 等角的余角相等 | |
| C． | 等式的两边同加上或同减去一个式子，结果仍为等式 | |
| D． | 如果a+b＞0，那么a＞0，b＞0 |
19．
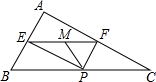如图，在△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为（ ）
如图，在△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为（ ）| A． | 1.2 | B． | 1.3 | C． | 1.4 | D． | 2.4 |
20．若A、B、C是直线l上的三点，P是直线l外一点，且PA=6cm，PB=5cm，PC=4cm，则点P到直线l的距离（ ）
| A． | 等于4cm | B． | 大于4cm而小于5cm | ||
| C． | 不大于4cm | D． | 小于4cm |