16．若等腰直角三角形的外接圆半径的长为$\sqrt{2}$.则其内切圆半径的长为( )A．$2\sqrt{2}-1$B．$2\sqrt{2}-2$C．$2-\sqrt{2}$D．$\sqrt{2}-——青夏教育精英家教网——

16．若等腰直角三角形的外接圆半径的长为$\sqrt{2}$，则其内切圆半径的长为（　　）

15．下列叙述正确的是（　　）

	A．	方差越大，说明数据就越稳定
	B．	一元二次方程x²-x+1=0有两个不相等的实数根
	C．	圆内接四边形对角互补
	D．	两边及其一边的对角对应相等的两个三角形全等

14．在Rt△ABC中，∠C=90°，AB=5，AC=3，则cosB的值为（　　）

13．在比例尺为1：50000的地图上量得甲、乙两地的距离为10cm，则甲、乙两地的实际距离是（　　）

12．一组数据1，2，3，0，-2，-3的极差是（　　）

如图，在平面直角坐标系xOy中，一次函数y=k₁x+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数y=kx的图象交点为C（3，4）．求：
（1）求k值与一次函数y=k₁x+b的解析式；
（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，请求出点D的坐标；
（3）在y轴上求一点P使△POC为等腰三角形，请求出所有符合条件的点P的坐标．

请你用学习“一次函数”时积累的经验和方法解决下列问题：
（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表填空：

x	…	-3	-2	-1	0	1	2	3	…
y	…								…

②描点、连线，画出y=|x|的图象；
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）写出函数y=|x|与y=|x+2|图象的平移关系．

甲、乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑电动车，甲到达B地停留半个小时后返回A地，如图是他们与A地之间的距离y（千米）与经过的时间x（小时）之间的函数关系图象．
（1）求甲从B地返回A地的过程中，y与x之间的函数关系式，并写出自变量x的取值范围；
（2）已知乙骑电动车的速度为40千米/小时，求乙出发后多少小时和甲相遇？

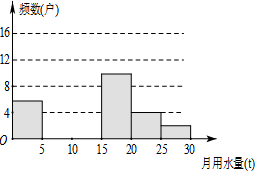八（1）班同学为了解2015年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，

月均用水量x（t）	频数（户）	频率
0＜x≤5	6	0.12
5＜x≤10	m	0.24
10＜x≤15	16	0.32
15＜x≤20	10	0.20
20＜x≤25	4	n
60≤x＜70	2	0.04

请解答以下问题：
（1）填空：m=12，n=0.08，并把频数分布直方图补充完整；
（2）若该小区有1000户家庭，求该小区月均用水量超过10t的家庭大约有多少户？

7．已知一次函数y=ax+b（a≠0）和y=kx（k≠0）图象交点坐标为（2，-3），则二元一次方程组 $\left\{\begin{array}{l}y-ax=b\\ y-kx=0\end{array}$的解是$\left\{\begin{array}{l}x=2\\ y=-3\end{array}\right.$．

0 280597 280605 280611 280615 280621 280623 280627 280633 280635 280641 280647 280651 280653 280657 280663 280665 280671 280675 280677 280681 280683 280687 280689 280691 280692 280693 280695 280696 280697 280699 280701 280705 280707 280711 280713 280717 280723 280725 280731 280735 280737 280741 280747 280753 280755 280761 280765 280767 280773 280777 280783 280791 366461