题目内容
9. 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们与A地之间的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们与A地之间的距离y(千米)与经过的时间x(小时)之间的函数关系图象.(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)已知乙骑电动车的速度为40千米/小时,求乙出发后多少小时和甲相遇?
分析 (1)首先设y与x之间的函数关系式为y=kx+b,根据图象可得直线经过(1.5,90),(3,0),利用待定系数法把此两点坐标代入y=kx+b,即可求出一次函数关系式;
(2)联立两个方程解答即可.
解答 解:(1)设甲从B地返回A地的过程中,y与x之间的函数关系式为y=kx+b,
根据题意得:$\left\{\begin{array}{l}{3k+b=0}\\{1.5k+b=90}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-60}\\{b=180}\end{array}\right.$,
所以y=-60x+180(1.5≤x≤3);
(2)由乙骑电动车的速度为40千米/小时,可得:y=40x,
由$\left\{\begin{array}{l}y=-60x+180\\ y=40x\end{array}\right.$,
解得$\left\{\begin{array}{l}x=1.8\\ y=72\end{array}\right.$,
答:乙出发后1.8小时和甲相遇.
点评 此题主要考查了一次函数的应用,关键是看懂图象所表示的意义,利用待定系数法求出甲从B地返回A地的过程中,y与x之间的函数关系式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
4.下列说法正确的是( )
| A. | 近似数3.58精确到十分位 | B. | 近似数1000万精确到个位 | ||
| C. | 近似数20.16万精确到0.01 | D. | 2.77×104精确到百位 |
14.在Rt△ABC中,∠C=90°,AB=5,AC=3,则cosB的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
18.在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OC的长度是( )
| A. | 1.5cm | B. | 2cm | C. | 4cm | D. | 6cm |
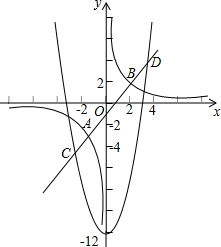 如图,已知双曲线C1:y=$\frac{1}{x}$、抛物线C2:y=x2-12,直线l:y=kx+m.
如图,已知双曲线C1:y=$\frac{1}{x}$、抛物线C2:y=x2-12,直线l:y=kx+m.