16. 已知二次函数y=2x2+4x-6.
已知二次函数y=2x2+4x-6.
(1)把函数配成y=a(x-h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
根据图象回答:
(4)当y≥0时,则x的取值范围为x≥1或x≤-3.
(5)当-3<x<0时,则y的取值范围为0>y≥-8.
 已知二次函数y=2x2+4x-6.
已知二次函数y=2x2+4x-6.(1)把函数配成y=a(x-h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
| x | … | … | |||||
| y | … | … |
(4)当y≥0时,则x的取值范围为x≥1或x≤-3.
(5)当-3<x<0时,则y的取值范围为0>y≥-8.
11.抛物线y=-(x+6)(x-4)的顶点坐标是( )
| A. | (-1,25) | B. | (-1,-25) | C. | (1,-21) | D. | (1,21) |
9.已知:$\frac{x+y}{x-2y}=\frac{5}{2}$,则$\frac{x}{y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | 3 | D. | 4 |
8.已知两个相似三角形的相似比为2:3,那么这两个三角形的面积之比为( )
| A. | 3:2 | B. | 4:6 | C. | 4:9 | D. | 2:3 |
7.某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:
由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为-90km,流动加油车出发位置为-80km;
(2)当两车同时开出x小时时,甲车位置为190-40xkm,流动加油车位置为-80+50x km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
0 278235 278243 278249 278253 278259 278261 278265 278271 278273 278279 278285 278289 278291 278295 278301 278303 278309 278313 278315 278319 278321 278325 278327 278329 278330 278331 278333 278334 278335 278337 278339 278343 278345 278349 278351 278355 278361 278363 278369 278373 278375 278379 278385 278391 278393 278399 278403 278405 278411 278415 278421 278429 366461
| 时间(h) | 0 | 5 | 7 | x |
| 甲车位置(km) | 190 | -10 | ||
| 流动加油车位置(km) | 170 | 270 |
(1)甲车开出7小时时的位置为-90km,流动加油车出发位置为-80km;
(2)当两车同时开出x小时时,甲车位置为190-40xkm,流动加油车位置为-80+50x km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
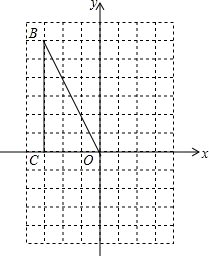 如图,已知O是坐标原点,B(-3,6),C(-3,0),以原点O为位似中心,将△OBC缩小为原来的一半(即新图形与原图形的相似比为1:2).
如图,已知O是坐标原点,B(-3,6),C(-3,0),以原点O为位似中心,将△OBC缩小为原来的一半(即新图形与原图形的相似比为1:2). 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).则正方形ABCD的面积为5,延长CB交x轴于点A1,作正方形A1B1C1C,则正方形A1B1C1C的面积为$\frac{45}{4}$;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,正方形A2015B2015C2015C2014的面积为5×${({\frac{9}{4}})^{2015}}$.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).则正方形ABCD的面积为5,延长CB交x轴于点A1,作正方形A1B1C1C,则正方形A1B1C1C的面积为$\frac{45}{4}$;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,正方形A2015B2015C2015C2014的面积为5×${({\frac{9}{4}})^{2015}}$.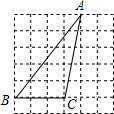 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠B的值为$\frac{5}{4}$.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠B的值为$\frac{5}{4}$. 在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{DB}=\frac{3}{5}$,DE=6,则BC的长度为( )
在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{DB}=\frac{3}{5}$,DE=6,则BC的长度为( )